时间:2017-11-05 17:51:25
1、计算题 一个内壁光滑的圆柱形气缸,质量为M,底面积为S。缸内有一个质量为m的活塞,封闭了一定质量的理想气体,不计活塞厚度。温度为t0时,如果用绳子系住活塞将气缸悬挂起来,如图(a)所示,气缸内气体柱的高为L1,如果用绳子系住气缸底,将气缸倒过来悬挂起来,如图(b)所示,气缸内气体柱的高为L2,设两种情况下气缸都处于竖直状态,求:当时的大气压强。
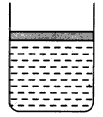
2、选择题 如图所示的容器,用活塞封闭着刚好饱和的一些水汽,测得水汽的压强为p,体积为V,当保持温度不变
[? ]
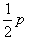
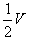 时,水汽的压强增为2p
时,水汽的压强增为2p 3、计算题 如图,一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封,上端封闭但留有一抽气孔。管内下部被活塞封住一定量的气体(可视为理想气体),气体温度为T1。开始时,将活塞上方的气体缓慢抽出,当活塞上方的压强达到p0时,活塞下方气体的体积为V1,活塞上方玻璃管的容积为2.6V1。活塞因重力而产生的压强为0.5p0。继续将活塞上方抽成真空并密封,整个抽气过程中管内气体温度始终保持不变,然后将密封的气体缓慢加热。求:
(1)活塞刚碰到玻璃管顶部时气体的温度;
(2)当气体温度达到1.8T1时气体的压强。 
4、简答题 长25cm的玻璃管,两端开口,竖直插在水银槽内,露在槽内水银面外玻璃管的长度为13cm.现将上端管口封闭,然后将玻璃管竖直向上全部提出水银柱面外,若温度保持不变,大气压强为75cmHg,则存在管内的水银柱的长度为多长?
5、计算题 如图所示,粗细均匀的U形管竖直放置,左端封闭,右端开口,左端用水银封闭着长L=18cm的理想气体,当温度为27℃时,两管水银面的高度差Δh=4cm,设外界大气压为75cmHg,为了使左、右两管中的水银面相平,
(1)若对封闭气体缓慢加热,温度需升高到多少℃;
(2)若温度保持27℃不变,向右管缓慢注入水银最后左、右两管的水银面相平且稳定时,气柱的长度是多少.