时间:2017-11-05 17:32:13
1、选择题 如图所示，质量为m的小球套在倾斜放置的固定光滑杆上，一根轻质弹簧的一端悬挂于O点，另一端与小球相连，弹簧与杆在同一竖直平面内，将小球沿杆拉到弹簧水平位置由静止释放，小球沿杆下滑，当弹簧位于竖直位置时，小球速度恰好为零，此时小球下降的竖直高度为h，若全过程中弹簧始终处于伸长状态且处于弹性限度范围内，下列说法正确的是(? )
A．弹簧与杆垂直时，小球速度最大
B．弹簧与杆垂直时，小球的动能与重力势能之和最大
C．小球下滑至最低点的过程中，弹簧的弹性势能增加量小于mgh
D．小球下滑至最低点的过程中，弹簧的弹性势能增加量等于mgh
参考答案：BD
本题解析：光滑杆没有摩擦力做功，杆的弹力和运动方向垂直也不做功，那么整个过程只有弹簧弹力和小球重力做功，二者组成的系统机械能守恒，分析小球的受力，在沿杆方向一个是自身重力分力另外一个是弹力沿杆方向的分力，当弹簧与杆垂直时，沿杆方向没有弹簧的分力，只有重力沿杆向下的分力，说明小球在沿杆向下加速，所以速度不竖直最大答案A错。由于全过程弹簧始终处于伸长状态那么弹簧与杆垂直时弹簧伸长量最小，弹性势能最小，根据小球弹簧系统机械能守恒，此时小球机械能最大，即动能和重力势能之和最大答案B对。从初位置到末位置，小球速度都是0动能不变，重力势能减速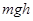
，根据系统机械能守恒，弹簧弹性势能增加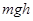答案D对C错。
本题难度：一般
2、填空题 （原创）．如图所示，一个半径为r的半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的，一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，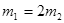
，让质量为m1的小球静止释放，当其到达碗底时质量为m2的小球速度为多大( )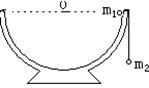
A．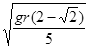
B．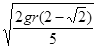
C．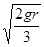
D．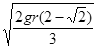
参考答案：B
本题解析：质量为m1的小球到达碗底时，设其速度大小为v1，质量为m2的小球速度大小为v2，如图所示，由几何关系，可知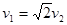
；把两个小球看成一个系统进行分析，由机械能守恒定律，可得
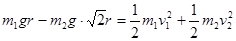，联立两式，可解得
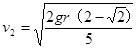，所以正确选项为B。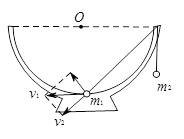
本题难度：一般
3、简答题 如图5－11所示，一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mB=m的小球连接，另一端与套在光滑直杆上质量mA=m的小物块连接，已知直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角θ=60°，直杆上C点与两定滑轮均在同一高度，C点到定滑轮O1的距离为L，重力加速度为g，设直杆足够长，小球运动过程中不会与其他物体相碰．现将小物块从C点由静止释放，试求：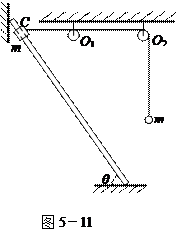
小题1:小球下降到最低点时，小物块的机械能（取C点所在的水平面为参考平面）；
小题2:小物块能下滑的最大距离；
小题3:小物块在下滑距离为L时的速度大小．
参考答案：
小题1: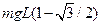
?
小题2: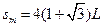
小题3: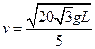
本题解析：
小题1:小球下降到最低点时速度为0，设此时小物块的机械能为E1．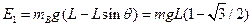
?
小题2:设小物块能下滑的最大距离为sm，此时小球、小物块速度为0，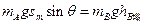
?
而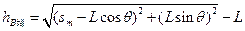
?
代入解得??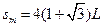
小题3:设小物块下滑距离为L时的速度大小为v，此时小球的速度大小为vB，则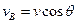
?
?
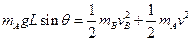解得?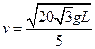
本题难度：一般
4、选择题 处于竖直向上匀强磁场中的两根电阻不计的平行金属导轨，下端连一电阻R，导轨与水平面之间的夹角为θ．一电阻可忽略的金属棒ab，开始固定在两导轨上某位置，棒与导轨垂直．如图所示，现释放金属棒让其由静止开始沿轨道平面下滑．就导轨光滑和粗糙两种情况比较，当两次下滑的位移相同时，则有（ ）
A．重力势能的减小量相同
B．机械能的变化量相同
C．磁通量的变化量相同
D．磁通量的变化率相同
参考答案：A、当两次下滑的位移相同时，重力做功相同，重力势能的减小量相同．故A正确．
? B、机械能的变化量不同．导轨粗糙时，ab棒所受阻力大，下滑加速度小，下滑的位移相同时，金属棒的速度小，机械能减小较大．故B错误．
? C、两次下滑的位移相同时，ab棒扫过的面积相同，磁通量的变化量相同．故C正确．
? D、轨光滑和粗糙两种情况比较，磁通量的变化率不同．导轨粗糙时，ab棒所受阻力大，下滑时间较长，磁通量变化率较小．故D错误．
故选AC
本题解析：
本题难度：简单
5、选择题 如图所示，倾角30°的斜面连接水平面，在水平面上安装半径为R的半圆竖直挡板，质量m的小球从斜面上高为R/2处静止释放，到达水平面恰能贴着挡板内侧运动。不计小球体积，不计摩擦和机械能损失。则小球沿挡板运动时对挡板的作用力是(? )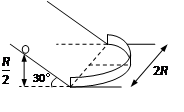 
A．0.5mg
B．mg
C．1.5mg
D．2mg
参考答案：B
本题解析：小球在下落过程中，受到重力和支持力的作用，其中支持力方向与运动方向始终垂直，不做功，只有重力做功，机械能守恒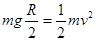
，
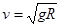,到达水平面后，挡板给小球的支持力提供向心力，
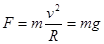，B选项正确。
点评：该类型题目中，支持力方向始终与物体运动方向垂直，即支持力永远不做功，类似的题目还有单摆中绳上的拉力等。本题目结合匀速圆周运动，考察向心力基本公式的应用。
本题难度：一般