时间:2017-09-26 11:02:10
1、简答题 受控核聚变过程中可释放出巨大的内能,对于参与核聚变的带电粒子而言,没有通常意义上的“容器”可装.科技工作者设计出了一种利用磁场约束带电粒子运动,使参与核聚变的带电粒子约束在某个区域内的控制方案,这个方案的核心可简化为如下的模型:如图所示是一个截面为内径R1=0.10m、外径R2=0.20m的环状区域,O点为该环状区域的圆心,区域内有垂直于截面向里的匀强磁场,磁感应强度B=0.50T.将带电粒子源置于环状区域内侧的A点(位于O点的正下方),若带电粒子源能沿垂直磁场方向连续地向各个方向射出氦核,已知氦核的比荷q/m=4.8×107C/kg,不计带电粒子之间的相互作用力及其所受的重力.
(1)若氦核从A点射出时的速度大小为4.8×105m/s,则它在磁场区域内做匀速圆周运动的半径为多大?
(2)若某氦核从A点射出后,恰好能沿磁场区域的内侧运动,则此氦核由A点射出时的速度大小和方向如何?
(3)假设粒子源向各个方向射出的氦核的最大速率都相同,若要使射入磁场的所有氦核都不能穿出磁场外边界,求氦核的最大速率.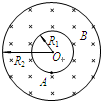
参考答案:(1)设氦核质量为m,电荷为q,以速度v在磁感应强度为B的匀强磁场中做半径为r的匀速圆周运动,由洛仑兹力公式和牛顿第二定律有:
? qvB=mv2r
解得:r=mvqB=2.0×10-2m
(2)因氦核带正电,且在磁场中做半径为R1的匀速圆周运动,所受洛仑兹力一定指向O点,根据左手定则可判断出,氦核在A点的速度方向为水平向右.
设此时氦核的速度为大小为v1,则由洛仑兹力公式和牛顿第二定律有:
? qvB=mv2R1
解得:v1=qBR1m=2.4×106m/s.
(3)当氦核以vm的速度沿与内圆相切的方向射入磁场且轨道与外圆相切时,则以速度vm沿各方向射入磁场区的氦核都不能穿出磁场外边界.由答图3中知此氦核的半径
? r′=R2-R12=0.05m.
由 qvB=mv2r,得?r=mvqB,
在速度为vm时不穿出磁场外边界应满足的条件是
? mvmqB≤r′
所以?vm≤qBr′m=1.2×106m/s.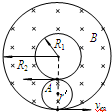
答:
(1)它在磁场区域内做匀速圆周运动的半径为2.0×10-2m.
(2)氦核由A点射出时的速度大小为2.4×106m/s,氦核在A点的速度方向为水平向右.
(3)氦核的最大速率是1.2×106m/s..
本题解析:
本题难度:一般
2、简答题 在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P(
3 |
| m q |
(1)匀强电场的场强E的大小; (2)撤去电场加上磁场的瞬间,微粒所受合外力的大小和方向; (3)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标值应满足什么条件? 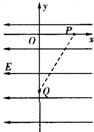 参考答案: 本题解析: 本题难度:一般 3、选择题 如图所示,质量为m 的小球在竖直平面内的光滑轨道上做圆周运动.圆的半径为R,小球经过圆环高点时刚好不脱离圆环,则其通过最高点时 参考答案:BCD 本题解析: 本题难度:一般 4、简答题 用长为L的细线拴一质量为m?的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向平角为θ,如图所示.求: 参考答案: 本题解析: 本题难度:一般 5、填空题 如图所示,a、b、c三个相同的小球系在同一根线上,Oa=ab=bc,当它们绕O点在光滑水平面上以相同的角速度作匀速圆周运动时,三段线中的拉力大小之比为Toa:Tab:Tbc=______. 参考答案:对c球,根据牛顿第二定律得,Tbc=m?rocω2, 本题解析: 本题难度:一般 |