时间:2017-09-26 10:18:58
1、简答题 (1)为了研究平抛运动在水平方向的运动情况,甲同学设计了一个如图(1)所示的实验.将两个同样的倾斜轨道固定在同一竖直面内,其下端水平,滑道2与光滑水平板平滑连接,把两个相同的小钢球从斜面的同一高度由静止释放,发现小球1恰能击中小球2,改变斜槽1的高度,或同步改变两小球的释放位置新进行实验,结果依然可以击中,这说明______.
(2)(多选)乙同学在研究平抛运动的轨道,实验装置如图(2)所示.关于这个实验,下列说法错误的是______
A.每次实验小球必须从同一高度静止释放,并且初始位置越高越好
B.斜槽必须光滑,末端必须水平
C.选用小球的质量大些,可供得更大的初速度
D.小球运动昧应与木板上的纸面相接触
(3)乙同学在实验中,用一张印有小方格的纸记录轨迹,小方格的边长为L,小球在平抛运动中的几个位置如图(3)中的a、b、c、d所示,则小球平抛初速度的计算式为______(用g、L表示)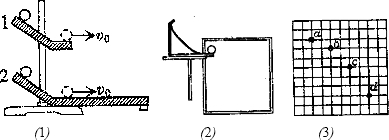
参考答案:(1)两次做平抛运动的小球都能击中下面做匀速直线运动的小球,说明在水平方向上两小球的运动情况相同.即:平抛运动在水平方向的分运动是匀速运动
(2)A:每次释放小球的位置必须相同且由静止释放小球,是为了使小球有相同的初速度且位置高了平抛运动的轨迹更好画,故A正确.
B:只有斜槽的末端保持水平,小球才具有水平初速度,其运动才是平抛运动,故B正确.
C:小球的质量越大,重力做功越多,初速度越大,平抛运动的轨迹更好画,故C正确.
D:如果小球在运动过程中与木板上的白纸相接触就会改变它的运动轨迹,使其不是平抛运动,故D错误.
故选:ABC
(3)竖直方向:自由落体运动,因时间相等,由△h=gt2可得:t=Lg
v0=2Lt=2
本题解析:
本题难度:一般
2、计算题 (14分)如图7所示,水平屋顶高H=5 m,墙高h=3.2 m,墙到房子的距离L=3 m,
墙外马路宽x=10 m,小球从房顶水平飞出,落在墙外的马路上,求小球
离开房顶时的速度v0的取值范围.(取g=10 m/s2) ? ?
?
参考答案:5 m/s≤v0≤13 m/s
本题解析:设小球恰好越过墙的边缘时的水平初速度为v1,
由平抛运动规律可知: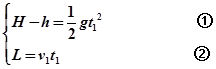
由①②得:v1=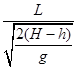 =
=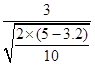 ?m/s
?m/s
=5 m/s
又设小球恰落到路沿时的初速度为v2,
由平抛运动的规律得: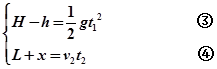
由③④得:v2=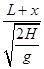 =
=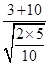 ?m/s=13 m/s
?m/s=13 m/s
所以小球抛出时的速度大小为5 m/s≤v0≤13 m/s.
本题难度:一般
3、选择题 如图所示,一网球运动员将球在边界处正上方水平向右击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法中正确的是?( )
A.击球点高度h1与球网高度h2之间的关系为h1=1.8h2
B.若保持击球高度不变,球的初速度V0只要不大于
| s h1 |
| 2gh1 |

参考答案:A、平抛运动在水平方向上做匀速直线运动,水平位移为s和3s2的时间比2:3,则竖直方向上,根据h=12gt2,则有h1-h2h1=49,解得h1=1.8h2.故A正确.
? B、若保持击球高度不变,要想球落在对方界内,要既不能出界,又不能触网,根据h1=12gt12得,t1=
本题解析:
本题难度:简单
4、选择题 在教学楼的楼梯口,有如图所示的0、1、2、3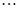 k级台阶,每级台阶的长为30cm,高为15cm(g=10m/s2).某同学从第0级台阶的边缘以v0=5m/s水平抛出一小球(不计一切阻力),则小球将落在第几级台阶上
k级台阶,每级台阶的长为30cm,高为15cm(g=10m/s2).某同学从第0级台阶的边缘以v0=5m/s水平抛出一小球(不计一切阻力),则小球将落在第几级台阶上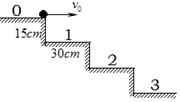
A.7级
B.8级
C.9级
D.10级
参考答案:C
本题解析:如图作一条连接各端点的直线,只要小球越过该直线,则小球落到台阶上;设小球落到斜线上的时间t,水平: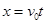 ,竖直:
,竖直: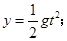 且
且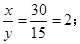 解得
解得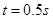
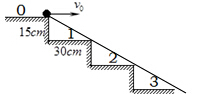
相应的水平距离: ,台阶数:
,台阶数: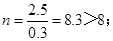 知小球抛出后首先落到的台阶为第9级台阶.故C正确
知小球抛出后首先落到的台阶为第9级台阶.故C正确
本题难度:简单
5、选择题 在倾角为30°高为h的斜面顶端,将一个小球沿水平方向抛出,抛出时小球的速度v=
| 2gh |
|
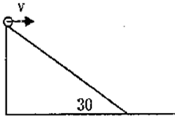
参考答案:A、位移与水平方向的夹角α的正切值为tanα=yx=12gt2v0t=gt2v0,
速度与水平方向的夹角β的正切值为tanβ=vyv0=gtv0,
所以tanβ=2tanα,
所以一定是α<β,所以A正确;
BC、当小球落到地面上时,竖直方向上的速度最大,速度与水平方向的夹角也是最大的,
此时,小球的运动的时间为t,
由h=12gt2,可得
t=
本题解析:
本题难度:简单