时间:2017-09-26 10:06:43
1、选择题 2009年10月6日,原香港中文大学校长、“光纤之父”高锟被宣布获得诺贝尔物理学奖.早在1996年中国科学院紫金山天文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”.假设高锟星的公转周期为T(T>1年),轨道半径为R,万有引力常量为G,则( )
A.高锟星公转的线速度大于地球公转的线速度
B.由上述数据可计算出太阳的质量
C.由上述数据可计算出太阳和高锟星之间的引力
D.地球和高锟星的轨道半径之比为
|
参考答案:A、根据万有引力提供向心力得:
GMmR2=m?4π2RT2,
T=2π
本题解析:
本题难度:简单
2、简答题 如图所示,在XOY直角坐标系中,OQ与OP分别与X轴正负方向成450,在POQ区域中存在足够大的匀强电场,场强大小为E,其余区域存在匀强磁场,一带电量为+q的质量为m粒子在Y轴上A点(0,-L)以平行于X轴速度v0进入第四象项,在QO边界垂直进入电场,后又从PO边界离开电场,不计粒子的重力.求:
(1)匀强磁场的磁感应强度大小?
(2)粒子从PO进入磁场的位置坐标?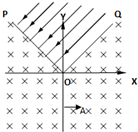
参考答案:(1)设磁感应强度为B,则在磁场中运动,根据牛顿第二定律有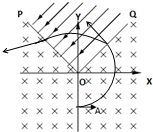
? qv0B=mv20r
由几何关系可得 r=L?
则B=mv0qL?
(2)设粒子在电场中运动的加速度大小为α,则根据牛顿第二定律有
? a=qEm?
由平抛运动规律知
OQ方向:r=12at2
OP方向:S=v0t
联立解得,S=v0
本题解析:
本题难度:一般
3、选择题 如图所示,在同一轨道平面上的几个质量不等的人造地球卫星A、B、C,均绕地球做匀速圆周运动,它们在某一时刻恰好在同一直线上,下列说法中正确的是( )
A.轨道线速度vA<vB<vC
B.万有引力FA>FB>FC
C.向心加速度aA>aB>aC
D.运动一周后,它们将同时回到图示位置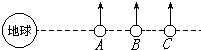
参考答案:A、根据GMmr2=ma=mv2r=mr(2πT)2知,轨道半径越大,向心加速度越小,线速度越小,周期越大.故A错误,C正确.
? B、因为不知道人造地球卫星A、B、C的质量大小关系,无法比较它们所受的万有引力.故B错误.
? D、三个人造卫星的周期不同,运动一周后,不会同时回到图示位置.故D错误.
故选C.
本题解析:
本题难度:简单
4、选择题 如图所示,在第一象限内有垂直纸面向里的匀强磁场,正、负电子分别以相同速度沿与x轴成30°角的方向从原点垂直磁场射入,则负电子与正电子在磁场中运动时间之比为( )
A.1:
| 3 |
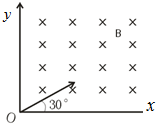
参考答案:正电子进入磁场后,在洛伦兹力作用下向上偏转,而负电子在洛伦兹力作用下向下偏转.由T=2πmqB,知两个电子的周期相等.
正电子从y轴上射出磁场时,根据几何知识得知,速度与y轴的夹角为60°,则正电子速度的偏向角为θ1=120°,其轨迹对应的圆心角也为120°,则正电子在磁场中运动时间为t1=θ1360°T=120°360°T=13T.
同理,知负电子以30°入射,从x轴离开磁场时,速度方向与x轴的夹角为30°,则轨迹对应的圆心角为60°,负电子在磁场中运动时间为t2=θ2360°T=60°360°T=16T.
所以负电子与正电子在磁场中运动时间之比为t2:t1=1:2.
故选B
本题解析:
本题难度:简单
5、计算题 在双人花样滑冰中,我们有时会看到女运动员被男运动员拉着做圆锥摆运动的精彩场面,如图所示,如果目测女运动员做圆锥摆运动时和竖直方向的夹角约为45 °,那么她所受的拉力约有多大?
参考答案:解:女运动员做圆锥摆运动时,重力和她所受的拉力的合力提供向心力,
拉力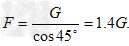
本题解析:
本题难度:一般