时间:2017-09-25 08:32:14
1、填空题 G是比例系数，叫做_____________，由英国物理学家_____________比较准确地测得G的数值，通常取G=_____________。
参考答案：引力常量，卡文迪许，6.67×10-11 N·m2/kg2
本题解析：
本题难度：简单
2、选择题 1970年4月24日，我国自行设计、制造的第一颗人造地球卫星“东方红一号”发射成功，开创了我国航天事业的新纪元．“东方红一号”的运行轨道为椭圆轨道，M是近地点，N是远地点，A、B是曲线M、N的中点．则（ ）
A．地球处在椭圆轨道的一个焦点上
B．卫星在M点的线速度大于N点的线速度
C．卫星在M点的加速度小于N点的加速度
D．卫星从A经M到B点运动时间与从B经N到A的运动时间相等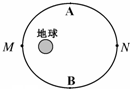
参考答案：A、根据开普勒第一定律，知地球处于椭圆轨道的一个焦点上．故A正确．
B、卫星从近地点向远地点N运动，万有引力做负功，动能减小，则卫星在M点的线速度大于N点的线速度．故B正确．
C、卫星在M点所受的万有引力大于在N点所受的万有引力，则卫星在M点的加速度大于在N点的加速度．故C错误．
D、由于卫星在近地点速度大，在远地点速度小，则卫星从A经M到B点运动时间小于从B经N到A的运动时间．故D错误．
故选AB．
本题解析：
本题难度：一般
3、选择题 已知万有引力常量G，根据下列已知条件能计算出地球质量的是（ ）
A．地球绕太阳运行的周期T和地球离太阳中心的距离R
B．人造地球卫星在地面附近运行的速度v和运行周期T
C．月球绕地球运行的周期T和月球离地球中心的距离R
D．地球半径R和地球同步卫星离地面的高度H（同步卫星周期已知）
参考答案：A、地球绕太阳做匀速圆周运动，受到太阳的万有引力充当向心力，用它运动周期表示向心力，由万有引力定律结合牛顿第二定律得：GM太mR2=m(2πT)2R，∴太阳的质量M太=4π2R3GT2，因此，不能求出地球的质量，故选项A错误．
B、人造卫星绕地球做匀速圆周运动，它受到地球的万有引力充当向心力，用它运动周期表示向心力，由万有引力定律结合牛顿第二定律得：GM地mR2=m(2πT)2R，又因T=2πRv，
∴地球的质量M地=Tv32πG，因此，可求出地球的质量，故选项B正确．
C、月球绕地球做匀速圆周运动，它受到地球的万有引力充当向心力，用它运动周期表示向心力，由万有引力定律结合牛顿第二定律得：GM地mR2=m(2πT)2R，∴地球的质量M地=4π2R3GT2，因此，可求出地球的质量，故选项C正确．
D、卫星绕地球做匀速圆周运动，它受到地球的万有引力充当向心力，用它运动周期表示向心力，由万有引力定律结合牛顿第二定律得：GM地m(R+H)2=m(2πT)2(R+H)，∴地球的质量M地=4π2(R+H)3GT2，因此，可求出地球的质量，故选项D正确．
故选BCD．
本题解析：
本题难度：简单
4、选择题 为了对火星及其周围的空间环境进行探测，我国预计于2011年10月发射第一颗火星探测器“萤火一号”．假设探测器在离火星表面高度分别为h1和h2的圆轨道上运动时，周期分别为T1和T2．火星可视为质量分布均匀的球体，且忽略火星的自转影响，万有引力常量为G．仅利用以上数据，可以计算出（ ）
A．火星的质量
B．“萤火一号”的质量
C．火星对“萤火一号”的引力
D．火星表面的重力加速度
参考答案：A、万有引力提供探测器做圆周运动所需的向心力，GMm(R+h1)2=m(R+h1)(2πT1)2，GMm(R+h2)2=m(R+h2)(2πT2)2，联立两方程，可求出火星的质量和半径．故A正确．
? B、“萤火一号”绕火星做圆周运动，是环绕天体，在计算时被约去，所以无法求出“萤火一号”的质量．故B错误．
? C、因为无法求出“萤火一号”的质量，所以无法求出火星对“萤火一号”的引力．故C错误．
? D、根据万有引力等于重力GMmR2=mg，可求出火星表面的重力加速度．故D正确．
故选AD．
本题解析：
本题难度：简单
5、计算题 有一颗绕地球做匀速圆周运动的卫星，到地心的距离为地球半径R0的2倍，卫星圆形轨道平面与地球赤道平面重合。已知地球表面重力加速度为g，近似认为太阳光是平行光，试估算：
（1）卫星做匀速圆周运动的周期；
（2）卫星绕地球一周，太阳能收集板工作时间
参考答案：（1）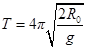
（2）
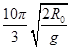
本题解析：（1）地球卫星做匀速圆周运动，轨道半径为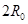
万有引力提供向心力：
?
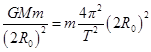在地球表面有：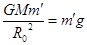
?
联立得卫星做匀速圆周运动的周期为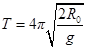
（2）如下图，当卫星在阴影区时不能接受阳光，据几何关系：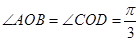
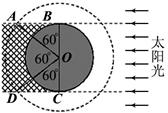
卫星绕地球一周，太阳能收集板工作时间为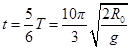
本题难度：一般