时间:2017-09-25 08:25:53
1、计算题 （1）（6分）氢原子的能级如图所示。氢原子从n=3能级向n=l能级跃迁所放出的光子，恰能使某种金属产生光电效应，则该金属的截止频率为____Hz；用一群处n=4能级的氢原子向低能级跃迁时所发出的光照射该金属，产生的光电子最大初动能为____ eV（普朗克常量h=6．63×10-34J"·s，结果均保留2位有效数字）。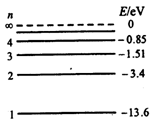
（2）（9分）如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内．a、b是轨道的两端点且高度相同，O为圆心。小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰。第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）。求A、B两球的质量之比mA:mB。（结果可以用根式表示）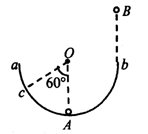
参考答案：(1)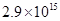
0.66? (2)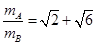
本题解析：（1）解决本题的关键是知道能级间跃迁辐射的光子能量等于两能级间的能级差．原子从能级n=3向n=1跃迁所放出的光子的能量为13.6-1.51=12.09eV，因所放出的光子，恰能使某种金属产生光电效应，则有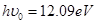
，解得：
．
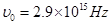当光子能量等于逸出功时，恰好发生光电效应，所以逸出功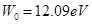
．
从n=4能级的氢原子向n=1跃迁所放出的光子能量最大，为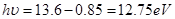
，
根据光电效应方程得 最大初动能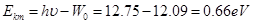
．
（2）小球B从静止下落至碰前过程只有重力做功，机械能守恒，设B与A碰前的速度大小为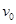
，则
由机械能守恒定律得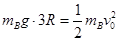 
设第一次碰撞后A、B的速度大小分别为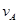
、
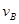，在第一次碰撞后B球恰返回到b点、A球上升的最高点c的过程中都只有重力做功，机械能守恒，由机械能守恒定律得
对小球A：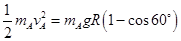
对小球B：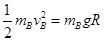
两球碰撞瞬间A、B组成的系统在水平方向上动量守恒，由动量守恒定律得：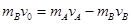
以上各式联立解得：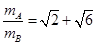
本题难度：一般
2、选择题 如图所示，某人以拉力F将物体沿斜面拉下，拉力大小等于摩擦力.则下列说法正确的是（ ?）
A．物体做匀变速运动
B．合外力对物体做功等于零
C．物体的机械能保持不变
D．物体的机械能减少
参考答案：AC
本题解析：拉力等于摩擦力，即两者做功之和为零，其中物体的支持力不做功，即仅有重力做功，说明满足机械能守恒条件，即C正确，但是合力不为零，合力做功不为零，做匀加速直线运动，A正确BD错误；
故选AC
点评：本题考查了对机械能守恒的条件的理解和判断，这类题型中平抛运动，匀速圆周运动常常是反例
本题难度：一般
3、计算题 如图所示，轻弹簧k一端与墙相连，处于自然状态，质量为4 kg的木块沿光滑的水平面以5m/s的速度运动并开始挤压弹簧.求弹簧的最大弹性势能及木块被弹回速度增大到3m/s时弹簧的弹性势能.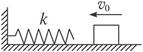
参考答案：32 J
本题解析：物体和弹簧构成的系统机械能守恒，当弹簧的弹性势能最大时，物体的动能为零，由机械能守恒定律得，弹簧的最大弹性势能为
Epm=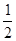
mv02=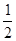×4×52 J="50" J （3分）
当物体的速度为v="3" m/s时，弹簧的弹性势能为Ep，由机械能守恒定律得
Ep+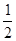mv2=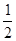mv02 （3分）
Ep=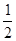mv02-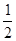mv2="50" J-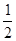×4×32 J="32" J.
点评：以弹簧和木块组成的系统为研究对象，只有弹力做功，系统的机械能守恒．初态时，系统只有木块的动能，当木块被弹回速度增大到3m/s时，木块有动能、弹簧有弹性势能，根据机械能守恒定律求解木块被弹回速度增大到3m/s时弹簧的弹性势能．
本题难度：一般
4、填空题 在距地面h=20m高处，以v=10m/s的速度将物体水平抛出，不计空气阻力，以地面为参考面，重力加速度g=10m/s2，物体质量为m=1kg，则抛出时物体的机械能为?J；落地时的动能为?J；在空中运动的时间为?s.
参考答案：250J? 250J? 2s
本题解析：抛出时的机械能为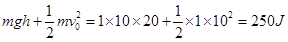
；由于下落过程中，机械能守恒，因此落地时的动能也是250J；由于下落过程中，竖直方向是自由落体运动，根据
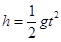可知落地时间
。
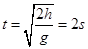本题难度：简单
5、选择题 (10分)如图所示，半径为R的
光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点．
求：（1）小球A滑到圆弧面底端时的速度大小．
（2）小球A撞击轻质弹簧的过程中，弹簧的最大弹性势能为多少．
参考答案：（1）
?（2）
本题解析：（1）设A球到达圆弧底端时的速度为v0，由机械能守恒定律有： 
?①（2分）?
A球到达圆弧底端时的速度?②（2分）
（2）当A、B两球速度相同时，弹簧的弹性势能最大，设共同速度为v（1分）
由动量守恒定律有：?
?③（2分）?
得
?④（1分）
由能量守恒可知，弹簧的最大弹性势能
?⑤（2分）
本题难度：一般