时间:2017-09-23 23:11:58
1、选择题 一小球以初速度v?0竖直上抛,它能到达的最大高度为H,问下列几种情况中,哪种情况小球不可能达到高度H(忽略空气阻力):?
A.图a,以初速v0沿光滑斜面向上运动
B.图b,以初速v0沿光滑的抛物线轨道,从最低点向上运动
C.图c(H>R>H/2),以初速v0沿半径为R的光滑圆轨道从最低点向上运动
D.图d(R>H),以初速v0沿半径为R的光滑圆轨道从最低点向上运动
参考答案:C
本题解析:根据机械能守恒定律,如果物体到达最高点时速度能为零,则物体一定能到达高H的地方。在上述四个图中a、b、d物体上升到最高点时的速度均可以为零,只有c因为超过了与圆心等高的位置后离开轨道做斜上抛运动,所以在最高点还有水平速度,所以不能达到高H的地方。
本题难度:一般
2、选择题 在下面列举的各个实例中,哪种情况机械能是守恒的?
A.汽车在水平面上加速运动
B.抛出的手榴弹或标枪在空中的运动(不计空气阻力)
C.拉着物体沿光滑斜面匀速上升
D.汽车关闭油门后沿水平公路向前滑行的过程
参考答案:B
本题解析:汽车在水平面上加速运动过程中牵引力做功,阻力做功,所以机械能不守恒,A错误;抛出的手榴弹在空中运动过程中,只受重力,只有重力做功,所以机械能守恒,B正确;
拉物体沿光滑斜面匀速上升过程中,拉力做功,所以机械能不守恒,C错误;
汽车关闭油门后沿水平公路向前滑行的过程,阻力做功,机械能不守恒,D错误
故选B
点评:物体机械能守恒的条件是只有重力或者是弹力做功,根据机械能守恒的条件逐个分析物体的受力的情况,即可判断物体是否是机械能守恒.
本题难度:简单
3、选择题 关于动量和动能的以下说法中正确的是( )
A.系统动量守恒的过程动能必定也守恒
B.系统动能守恒的过程动量必定也守恒
C.如果一个物体的动量保持不变,那么它的动能必然也不变
D.如果一个物体的动能保持不变,那么它的动量必然也不变
参考答案:A、系统动量守恒的表达式为m1v1+m2v2=m1v′1+m2v′2,而动能守恒的表达式为12m1v12+12m2v22=12m1v′12+12m2v′22,两者之间没有必然的联系,故AB错误;
C、动能的表达式EK=12mv2,动量P=mv,动能与动量之间的大小关系:Ek=P22m,一物体的动量P不变,其动能Ek一定不变,故C正确.
D、一物体的动能不变,其动量大小一定不变,但速度的方向可以变化,即动量的方向可以变化.故D错误.
故选C
本题解析:
本题难度:一般
4、计算题 AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,如图所示。一小球自A点起由静止开始沿轨道下滑。已知圆轨道半径为R,小球的质量为m,不计各处摩擦。求:
(1)小球运动到B点时的动能;
(2)小球下滑到距水平轨道的高度为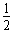 R时的速度大小和方向;
R时的速度大小和方向;
(3)小球经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大? 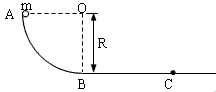
参考答案:解:(1)根据机械能守恒 Ek=mgR
(2)根据机械能守恒 ΔEk=ΔEp? mv2=
mv2=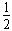 mgR?
mgR?
小球速度大小 v= ,速度方向沿圆弧的切线向下,与竖直方向成30°
,速度方向沿圆弧的切线向下,与竖直方向成30°
(3)根据牛顿运动定律及机械能守恒,在B点?
NB-mg=m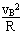 ,mgR=
,mgR=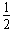 mvB2?
mvB2?
解得 NB=3mg,在C点:NC=mg
本题解析:
本题难度:困难
5、计算题 在水平地面上竖直固定一根内壁光滑的圆管,管的半径R=3.6m(管的内径大小可以忽略),管的出口A在圆心的正上方,入口B与圆心的连线与竖直方向成60°角,如图所示.现有一只质量m=1kg的小球(可视为质点)从某点P以一定的初速度水平抛出,恰好从管口B处沿切线方向飞入,小球到达A时恰好与管壁无作用力.取g=10m/s2.求: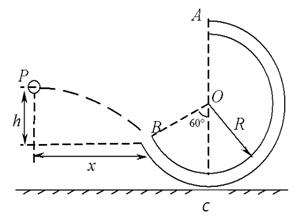
(1)小球到达圆管最高点A时的速度大小;
(2)小球在管的最低点C时,管壁对小球的弹力大小;
(3)小球抛出点P到管口B的水平距离x.
参考答案:(1)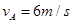 (2)
(2)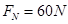 ,方向竖直向上(3)
,方向竖直向上(3)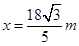
本题解析:(1)小球在最高点时,对管壁无作用力,根据向心力公式可得: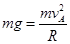
可得小球到达圆管最高点时的速度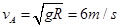
(2)设最低点C的速度为v,小球从管的最低点到最高点A,有机械能守恒定律可得: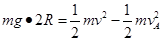 ,解得
,解得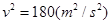
在最低点,由向心力公式可得: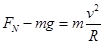
可得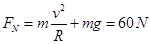 ,方向竖直向上
,方向竖直向上
(3)设B点的速度为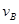 ,由机械能守恒定律 可得:
,由机械能守恒定律 可得: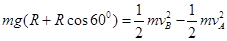
解得: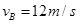
由平抛运动规律可知,小球做平抛运动过程的初速度 ,
,
在B点的竖直速度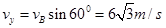 ,根据
,根据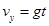 可得
可得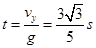
根据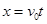 可知:小球的抛出点到管口B的水平距离
可知:小球的抛出点到管口B的水平距离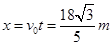
本题难度:一般