时间:2017-08-22 03:10:06
1、选择题 如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使其在瞬时得到一个水平初速v0,若v0≤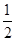 ,则有关小球能够上升到最大高度(距离底部)的说法中正确的是:(?)
,则有关小球能够上升到最大高度(距离底部)的说法中正确的是:(?)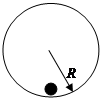
A.一定可以表示为v02/2g
B.可能为R/3
C.可能为R
D.可能为5R/3
参考答案:BC
本题解析:小球在运动过程中,机械能守恒,则有: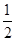 mv02=mgh解得:h≤
mv02=mgh解得:h≤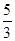 R,根据竖直平面内的圆周运动知识可知小球在上升到
R,根据竖直平面内的圆周运动知识可知小球在上升到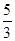 R之前就做斜抛运动了,所以最大高度不可能是
R之前就做斜抛运动了,所以最大高度不可能是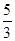 R,AD错误;由圆周运动的知识可知,小球在与圆心高度等高或小于圆心高度时的速度是可以为零的,所以若v0≤
R,AD错误;由圆周运动的知识可知,小球在与圆心高度等高或小于圆心高度时的速度是可以为零的,所以若v0≤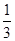 ,则有关小球能够上升到最大高度可以为R,也可以为
,则有关小球能够上升到最大高度可以为R,也可以为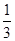 R,BC正确.
R,BC正确.
本题难度:一般
2、选择题 下面的实例中,机械能守恒的是( )
A.小球自由下落,不计空气阻力
B.拉着物体沿光滑的斜面匀速上升
C.跳伞运动员张开伞后,在空中匀速下降
D.飞行的子弹射入放在光滑水平桌面上的木块中
参考答案:A、小球自由下落,不计空气阻力,只有重力做功,机械能守恒,故A正确;
B、由于物体匀速上升,对物体受力分析可知,物体必定受到除重力之外的力的作用,并且对物体做了正功,所以物体的机械能增加,故B错误;
C、跳伞运动员张开伞后,在空中匀速下降,所以运动员要受到空气阻力的作用,故人的机械能在减小,所以C错误;
D、飞行的子弹击中放在光滑水平桌面上木块的过程中,子弹受到木块的阻力的作用,所以子弹的机械能减小,所以D错误;
故选A.
本题解析:
本题难度:简单
3、简答题 24.(17分)某宇航员在地球表面和某星球表面分别用如图所示同样装置做同样的实验,一小球静止在固定的竖直光滑圆弧内轨道的最低点,当分别给小球一个初速度时,都恰好使小球在竖直平面内做完整的圆周运动。现已知在地球做实验时,小球通过最高点的速度大小和在星球上做实验时小球在最低点的速度大小相等,若在该星球表面发射一颗卫星,所需的最小发射速度是多少?(星球半径为R,地球半径未知,万有引力常量为G,地球表面重力加速度为g) ?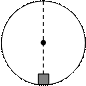
参考答案: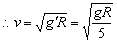
本题解析:设圆弧轨道半径为r,星球上重力加速度为g"
地球上最高点的速度为v1,星球上最高点的速度为v2
地球上: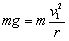 ? ……(2分)?星球上:
? ……(2分)?星球上: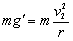 ? …(2分)
? …(2分)
在星球上由机械能守恒定律: ? ………(3分)
? ………(3分)
由题意: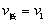 ?解得:
?解得: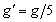 ? ………(3分)
? ………(3分)
对星球的近地卫星: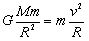 ?而
?而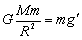 ? ………(4分)
? ………(4分)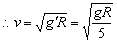 ? ………(3分)
? ………(3分)
本题难度:一般
4、计算题 (12分)如图所示,质量为M、内有半径R的半圆形轨道的槽体放在光滑的平台上,左端紧靠一台阶,质量为m的小物体从A点由静止释放,若槽内光滑。 求: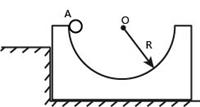
(1)小物体滑到圆弧最低点时的速度大小v
(2)小物体滑到圆弧最低点时,槽体对其支持力N的大小
(3)小物体上升的最大高度h
参考答案:(1)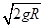 ;(2)
;(2)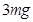 ;(3)
;(3)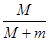 R
R
本题解析:(1)设小物体由A落至圆弧最低点时的速度为v,取圆弧最低点为势能零点,
由机械能守恒定律得:mgR=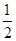 mv2?2分
mv2?2分
得v=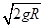 ?1分
?1分
(2)在最低点对小球受力分析,由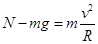 得:? 2分
得:? 2分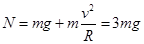 ? 1分
? 1分
(3)小物体向上运动的过程中,m与M组成的系统在水平方向的动量守恒:
设小球滑至最高点时m与M的共同速度为v′
所以? mv=(M+m)v′?2分
解得:v′=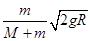 ?1分
?1分
此过程中系统机械能守恒,所以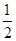 mv2-
mv2-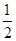 (M+m)v′2=mgh?2分
(M+m)v′2=mgh?2分
解得m上升的最大高度h=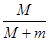 R.? 1分
R.? 1分
本题难度:一般
5、计算题 如图所示,长为R的轻绳,上端固定在O点,下端连一小球。小球接近地面,处于静止状态。现给小球一沿水平方向的初速度v0,小球开始在竖直平面内做圆周运动。设小球到达最高点时绳突然断开。已知小球最后落在离小球最初位置2R的地面上。求:
(1)小球在最高点的速度v;
(2)小球的初速度v0;
(3)小球在最低点时球对绳的拉力;
(4)如果细绳转过60°角时突然断开,则小球上升到最高点时的速度多大?(小球的质量为m,重力加速度为g)。 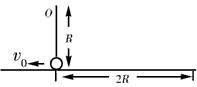
参考答案:解:(1)在水平方向有2R=vt
在竖直方向有2R=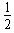 gt2
gt2
解得v=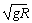
(2)根据机械能守恒定律有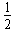 mv02-
mv02-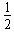 mv2=mg2R
mv2=mg2R
解得v0=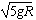
(3)对小球分析有F-mg=m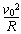
解得F=6mg
由牛顿第三定律可知:小球对绳子的拉力为6mg,方向向下
(4)设绳断时的速度为v1,有mgR(1-cos60°)= mv02-
mv02-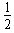 mv12
mv12
设小球在最高点时的速度为v2,有v2=v1cos60°
v2=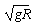
本题解析:
本题难度:一般