时间:2017-08-22 02:58:00
1、简答题 如图所示，质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端栓在固定挡板P上，另一端与靶盒A连接．Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度为v0=50m/s，质量m=0.010kg的弹丸，当弹丸打入靶盒A后，便留在盒内，碰撞时间极短．不计空气阻力．求：弹丸进入靶盒A后，弹簧的最大弹性势能为多少？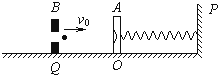
参考答案：（1）弹丸进入靶盒A后，弹丸与靶盒A的共同速度设为v，由系统动量守恒得：
mv0=（m+M）v
靶盒A的速度减为零时，弹簧的弹性势能最大，由系统机械能守恒得：
Ep=12（m+M）v2
解得：Ep=m22(m+M)v02
代入数值得Ep=2.5J
答：弹丸进入靶盒A后，弹簧的最大弹性势能为2.5J．
本题解析：
本题难度：一般
2、选择题 如图,长为a的轻质细线,一端悬挂在O点,另一端接一个质量为m的小球(可视为质点),组成一个能绕O点在竖直面内自由转动的振子.现有3个这样的振子,以相等的间隔b(b>2a)在同一竖直面里成一直线悬于光滑的平台MN上,悬点距台面高均为a.今有一质量为3m的小球以水平速度v沿台面射向振子并与振子依次发生弹性正碰,为使每个振子碰撞后都能在竖直面内至少做一个完整的圆周运动,则入射小球的速度v不能小于(? )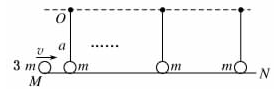
A．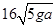
B．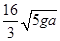
C．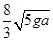
D．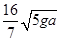
参考答案：C
本题解析：3m和m弹性碰撞:3mv=3mv′+mv1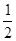
×3mv2=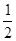×3mv′2+
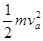,得v′=
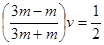
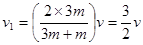
同理3m与第二个m弹性碰撞后得v″=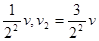
3m与第三个球碰后得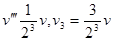
所以va>vb>vc,只要第三个球能做完整的圆周运动,则前两球一定能做完整的圆周运动.第三个球碰后,由机械能守恒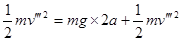
而
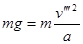,解之得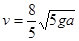
故C正确，故选C
点评：本题难度较小，应用动量守恒定律求解问题时，首先应明确研究系统，判断初末状态动量
本题难度：一般
3、选择题 三木块从同一高度同时开始自由下落，其中木块甲自由落体；木块乙在刚刚开始下落时被一颗子弹沿水平方向击中并留在其中；木块丙在下落途中被一颗子弹沿水平方向击中并留在其中。不计空气阻力及子弹进入木块的时间，则（?）
A．三块木块同时落地
B．甲木块最先落地，乙、丙同时落地
C．木块丙最后落地，甲、乙同时落地
D．甲、乙、丙依次先后落地
参考答案：C
本题解析：略
本题难度：简单
4、简答题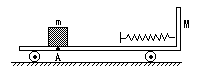 
图所示，在水平光滑的平面上停着一辆平板小车，小车质量M=10kg，在小车上的A处放有质量m=5kg的小滑块，现给小滑块一个瞬时冲量，使它获得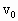
=6m／s的初速度在平板上滑行，与固定在平板车上的弹簧作用后又弹回，最后刚好回到A点与车保持相对静止，在此过程中小滑块相对于小车通过的总路程s=3m，g=10
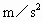，试求：
(1)弹簧在压缩过程中所具有的最大弹性势能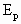
；
(2)小滑块与平板车之间的动摩擦因数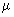
．
参考答案：
（1）30J?（2）0.4
本题解析：
(1)滑块m滑至弹簧压缩量最大时，有：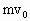
=(m＋M)v，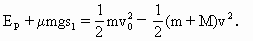
m滑回A点时，与小车共同运动的速度仍为v，有：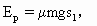
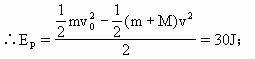
本题难度：一般
5、实验题 某同学用如图所示的（a）图装置来探究碰撞中的守恒量，图中PQ是斜槽，QR为水平槽，（b）图是多次实验中某球落到位于水平地面记录纸上得到10个落点痕迹，有关该实验的一些说法，不正确的有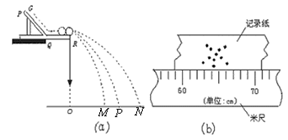
A．入射球和被碰球必须是弹性好的，且要求两球的质量相等，大小相同
B．被碰球静止放在槽口，入射球必须每次从轨道的同一位置由静止释放
C．小球碰撞前后的速度不易测量，所以通过测小球“平抛运动的射程”间接地解决
D．图（b）可测出碰撞后某球的水平射程为64.7cm（或取64.2cm — 65.2cm之间某值）
参考答案：A
本题解析：为防止两球碰撞后入射球反弹，入射球的质量应大于被碰球的质量，为发生对心碰撞，两球半径应相等，故A错误；为保证小球的速度相等，被碰球静止放在槽口，入射球必须每次从轨道的同一位置由静止释放，故B正确；小球离开轨道后做平抛运动，由于小球抛出点的高度相等，它们在空中的运动时间相等，小球的水平位移与小球的初速度成正比，小球碰撞前后的速度不易测量，所以通过测小球“平抛运动的射程”间接地解决，故C正确；由图示刻度尺可知，图（b）可测出碰撞后某球的水平射程为64.7cm（64.2cm-65.2cm均正确），故D正确；
本题难度：一般