时间:2017-08-22 02:34:37
1、选择题 一个小孩站在船头,按如图所示的两种情况用同样大小的力拉绳,若经过相同的时间t(设船未碰撞),小孩所做的功分别为W1、W2,在时间t末小孩拉绳的瞬时功率分别为P1、P2,则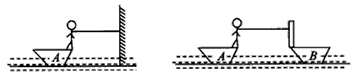
[? ]
A. W1>W2,P1>P2
B. W1=W2,P1=P2
C.W1<W2,P1<P2
D.W1<W2,P1=P2
参考答案:C
本题解析:
本题难度:一般
2、选择题 设轮船行驶时,受到的阻力f跟它的速度大小v成正比.如果轮船匀速行驶的最大速度是vm时发动机的功率为P,那么,要想把轮船行驶的最大速度提高到2vm,则发动机的功率应该提高到( )
A.2P
B.3P
C.4P
D.4.5?P
参考答案:轮船匀速行驶的最大速度是vm时,有P=fvm=kvm2.
当轮船行驶的最大速度提高到2vm,阻力f′=2kvm,则发动机的功率P′=f′?2vm=4kvm2=4P.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:简单
3、简答题 有一质量m=1000kg的轿车,在平直公路上以ν1=90km/h的速度匀速行驶,此时发动机的输出功率P=50kW,全部用于轿车的牵引.某时刻起,保持发动机的输出功率不变,启动利用电磁阻尼带动的电动机为车载蓄电池充电,轿车做减速运动.运动L=72m后,轿车速度变为ν2=72km/h,此过程中发动机输出功率的20%用于轿车的牵引,80%用于供给发电机工作,发电机获得能量的50%转化为蓄电池的电能.假设轿车在上述运动过程中所受阻力保持不变.
(1)求轿车运动中受到的阻力F阻的大小;
(2)求在上述过程中蓄电池获得的电能E电的大小;
(3)若该车可以利用所储存的电能作为动力来源,则轿车仅用上述过程中获得的电能E电维持匀速运动,能行驶的距离L’的大小是多少?
参考答案:(1)v1=90km/h=25m/s,v2=72km/h=20m/s.
匀速行驶时,P=F阻v1
则F阻=Pv1=5000025N=2×103N.
(2)设这一过程中汽车发动机做的总功为W,根据动能定理得:
20%W-W阻=12mv22-12mv12
代入数据得,W=1.575×105J
E电=50%×80%W=6.3×104J
(3)汽车维持匀速运动,电能全部克服阻力做功.
E电=F阻L′,代入数据得,L′=31.5m.
答:(1)轿车运动中受到的阻力F阻的大小为2×103N.
(2)上述过程中蓄电池获得的电能E电的大小为 6.3×104J.
(3)能行驶的距离L’的大小是31.5m.
本题解析:
本题难度:一般
4、选择题 如图,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A下落、B沿斜面下滑,则从剪断轻绳到物块着地,两物块( )
A.速率的变化量不同
B.机械能的变化量不同
C.重力势能的变化量相同
D.重力做功的平均功率相同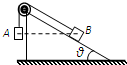
参考答案:设斜面倾角为θ,刚开始AB处于静止状态,所以mBgsinθ=mAg,所以mB>mA,
A、剪断轻绳后A自由下落,B沿斜面下滑,AB都只有重力做功,根据动能定理得:
12mv2=mgh
v=
本题解析:
本题难度:简单
5、简答题 A、B两车在同一直线上运动,质量为103Kg的A车在前,以恒功率80KW从静止开始行驶,行驶过程所受阻力为104N,经3s后速度达到稳定.之后在后面的B车以速度vB=16m/s与A车同向行驶,当A、B两车相距x=20m时,B车开始刹车,做匀减速运动.计算过程g=10m/s2
(1)A车从开始行驶到速度稳定时经过的路程x是多少?
(2)为避免两车相撞,刹车后B车的阻力至少应为车总重的多少倍?
参考答案:(1)对A车,根据动能定理,有:
Pt-fs=12mv2-0 ①
A车达到最大速度时,根据平衡条件,有:
F-f=0 ②
功率为:
P=Fv ③
联立解得:
v=8m/s
s=20.8m
(2)以以A车为参考系,B车做匀减速直线运动,初速度:16-8=8m/s,末速度为零,位移为20m,根据速度位移关系公式,有:
-v20=2ax
解得:
a=-v202x=-822×20=-1.6m/s2
根据牛顿第二定律,有:
-f=ma
故:
fmg=-ag=1.610=0.16
答:(1)A车从开始行驶到速度稳定时经过的路程s是20.8m;
(2)为避免两车相撞,刹车后B车的阻力至少应为车总重的0.16倍.
本题解析:
本题难度:一般