时间:2017-08-22 02:05:31
1、选择题 在闭合线圈上方有一条形磁铁自由下落直至穿过线圈过程中,下列说法中正确的是( )
A.磁铁下落过程中机械能守恒
B.磁铁下落过程中机械能增加
C.磁铁下落过程中机械能减少
D.线圈中增加的内能是由磁铁减少的机械能转化而来的
参考答案:CD
本题解析:
本题难度:简单
2、简答题 如图所示,两根金属导轨平行放置在倾角为θ=30°的斜面上,导轨左端接有电阻R=8Ω,导轨自身电阻不计.匀强磁场垂直于斜面向上,磁感应强度为B=0.5T.质量为m=0.1kg,电阻为r=2Ω的金属棒ab由静止释放,沿导轨下滑,如图所示.设导轨足够长,导轨宽度L=2m,金属棒ab下滑过程中始终与导轨接触良好,受到的摩擦阻力f=0.3N,当金属棒下滑的高度为h=3m时,恰好达到最大速度,g取10m/s2,求此过程中:
(1)金属棒的最大速度;
(2)电阻R中产生的热量;
(3)通过电阻R的电量.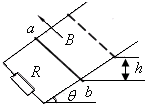
参考答案:(1)金属棒做匀速直线运动时,速度达到最大,设为v.
感应电动势:E=BLv,
电流:I=ER+r,
安培力:F=BIL=B2L2vR+r,
由平衡条件得:mgsinθ=F+f,
代入数据解得:v=2m/s;
(2)由能量守恒定律得:
mgh=Q+f?hsinθ+12mv2,
代入数据解得:Q=1J,
R上产生的热量:
QR=RR+rQ=88+2×1=0.8J;
(3)由法拉第电磁感应定律得:
E=△Φ△t=B?S△t=B?L?hsinθR+r,
电流:I=ER+r,
电荷量:q=I△t,
代入数据解得:q=0.6C;
答:(1)金属棒的最大速度为2m/s;
(2)电阻R中产生的热量为0.8J;
(3)通过电阻R的电量为0.6C.
本题解析:
本题难度:一般
3、简答题 如图所示,间距L=1m的足够长的光滑平行金属导轨与水平面成30°角放置,导轨电阻不计,导轨上端连有R=0.8Ω的电阻,磁感应强度为B=1T的匀强磁场垂直导轨平面向上,t=0时刻有一质量m=1kg,电阻r=0.2Ω的金属棒,以v0=10m/s的初速度从导轨上某一位置PP"开始沿导轨向上滑行,金属棒垂直导轨且与导轨接触良好,与此同时对金属棒施加一个沿斜面向上且垂直于金属棒的外力F,使金属棒做加速度大小为2m/s2的匀减速直线运动,则:
(1)t=2s时,外力F的大小?
(2)若已知金属棒运动从开始运动到最高点的过程中,电阻R上产生的热量为100J,求此过程中外力F做的功?
(3)到最高点后,撤去外力F,经过足够长时间后,最终电阻R上消耗的热功率是多少?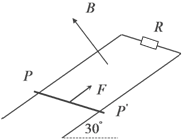
参考答案:(1)金属棒匀加速上升,根据速度时间关系公式,有:
v1=v0+at=10-2×2=6m/s
对金属棒受力分析,受重力、支持力、安培力,如图所示: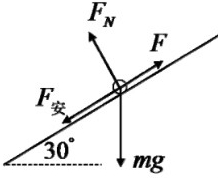
根据平衡条件,有:
mgsin30°+F安-F=ma
其中:
F安=BI1L
I1=E1R+r
E1=BLv1
解得:F=9N
(2)根据速度位移关系公式,到最高点的位移:
x=0-v202a=25m
由动能定理,得:
WF-mgxsin30°-Q总=0-12mv20
其中:Q总=R+rRQR=125J
解得:WF=200J
(3)如图所示,最后稳定时导体棒的速度满足:
mgsin30°=B2L2vR+r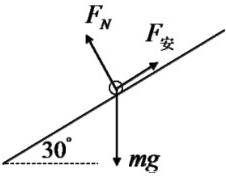
电功率等于克服安培力做功的功率,故:
P电=P安=mgvsin30°=25W
根据功率分配关系,有:
PR=RR+rP电=20W
答:(1)t=2s时,外力F的大小为9N;(2)此过程中外力F做的功为200J;(3)电阻R上消耗的热功率是20W.
本题解析:
本题难度:一般
4、选择题 如图所示,闭合金属环从高h的曲面滚下,又沿曲面的另一侧上升,设闭合环初速为零,摩擦不计,则( )
A.若是匀强磁场,环滚上的高度小于h
B.若是匀强磁场,环滚上的高度等于h
C.若是非匀强磁场,环滚上的高度等于h
D.若是非匀强磁场,环滚上的高度小于h
参考答案:BD
本题解析:若是匀强磁场,磁通量不变,没有感应电流产生,小球的机械能守恒,B对;若是非匀强磁场,穿过圆环的磁通量发生变化,有电流产生,有焦耳热产生,由能量守恒定律可知环滚上的高度小于h,D对;
本题难度:一般
5、选择题 如图所示,一光滑平行金属轨道平面与水平面成θ角,两导轨上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道平面向上.质量为m的金属杆ab,以初速v0从轨道底端向上滑行,滑行到某一高度h后又返回到底端.若运动过程中,金属杆保持与导轨垂直且接触良好,并不计金属杆ab的电阻及空气阻力,则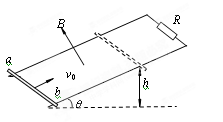
A.上滑过程中重力所做的功的绝对值大于下滑过程
B.上滑过程通过电阻R产生的热量比下滑过程多
C.上滑过程通过电阻R的电量比下滑过程多
D.上滑过程的时间比下滑过程长
参考答案:B
本题解析:重力做功只与始末位置的有关,由于金属杆又返回到底端,可见上滑和下滑过程始末位置相同,重力做功相同,A错;电阻R上产生的热量是由安培力做功转化而来,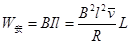 ,上滑和下滑过程中,位移L相同,由于安培力做负功,上滑过程的平均速度大于下滑过程的平均速度,位移相同,故上滑过程通过所用的时间小于下滑过程所用时间,同理电阻R产生的热量比下滑过程多,B对、D错;由
,上滑和下滑过程中,位移L相同,由于安培力做负功,上滑过程的平均速度大于下滑过程的平均速度,位移相同,故上滑过程通过所用的时间小于下滑过程所用时间,同理电阻R产生的热量比下滑过程多,B对、D错;由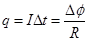 可知,上滑过程和下滑过程通过电阻R的电量相同,C错。
可知,上滑过程和下滑过程通过电阻R的电量相同,C错。
考点:本题考查了电磁感应现象中的功能关系。
本题难度:一般