时间:2017-08-22 02:00:22
1、简答题 如图所示，在水平面上有一质量为m的物体，在水平拉力作用下由静止开始运动一段距离后到达一斜面底端，这时撤去外力物体冲上斜面，上滑的最大距离和在平面?上移动的距离相等，然后物体又沿斜面下滑，恰好停在平面上的出发点．已知斜面倾角θ=300，斜面与平面上的动摩擦因数相同．
（1）求物体开始受的水平拉力F？
（2）物体运动全过程用v-t图象表示，并画在坐标纸上．
参考答案：（1）对于物体从开始运动到返回的整个过程，根据动能定理，有
F?L-2μmg?L-2μmgcos30°?L=0
对从最高点到返回出发点过程，有：
mgxsin30°-μmgcos30°x-μmgx=0
解得：μ=2-
本题解析：
本题难度：一般
2、计算题 一个热气球与沙包的总质量为60kg，在空气中以加速度=5m/s2下降。求（1）为了使它匀速下降，应抛掉沙的质量是多少？（2）为了使它以同样大小的加速度上升，应抛掉沙的质量是多少？（取g=10m/s2）
参考答案：（1）Δm=30kg（2）Δm1="40" kg
本题解析：（1）设浮力为F，以加速度a=5m/s2下降时有：
mg-F=ma? ···················（2分）
设匀速下降时系统总质量为m1，则有 m1g-F=0? ···················（3分）
应抛掉沙的质量为：? Δm="m-" m1?···················（2分）
由以上三式代入数据得? Δm=30kg? ···················（1分）
（2）设以同样大小的加速度上升时系统总质量为m2，则有? F- m2g= m2a? ···················（3分）
应抛掉沙的质量为? Δm1=" m-" m2?···················（2分）
代入数据得? Δm1="40" kg? ···················（1分）
本题考查对牛顿第二定律的应用，在热气球加速下降的过程中由重力和浮力的合力提供加速度，由牛顿第二定律可求得此时的浮力大小，抛掉沙之后重力减小，浮力不变，合力向上，能保证热气球向上加速，由牛顿第二定律可求得抛掉的沙的质量
本题难度：简单
3、计算题 如图所示为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送带的A 、B两端相距3m，另一台倾斜传送带的C、D两端相距4m，且与地面的倾角为37°，B、C相距很近。水平传送带以5m/s的速度沿顺时针方向转动，现将质量为10kg的一袋大米无初速度地放在A端，它随传送带到达B端后，速度大小不变地传到倾斜传送带的C点，米袋与两传送带间的动摩擦因数均为0.5，g取10m/s2，sin37°=0.6，cos37°=0.8。
（1）若倾斜传送带不运转，求米袋沿传送带在CD上所能上升的最大距离；
（2）若倾斜传送带也以5m／s的速率顺时针方向转动，求米袋从C运动到D所用的时间。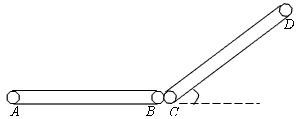 
参考答案：解：（1）米袋在AB上加速运动时，根据牛顿第二定律得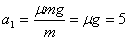
m/s2
米袋能达到的最大速度为v=5m／s时，滑行的距离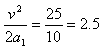
m＜3m，因此米先加速2.5m后与传送带一起匀速运动到达B点，到达C点时速度v1=5m／s，设米袋在静止的倾斜传送带上运动的加速度为a2，由牛顿第二定律得
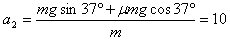m/s2
所以，它能上滑的最大距离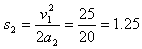
m?
（2）米袋滑上沿顺时针方向转动的倾斜传送带的C点时，米袋相对传送带静止，但米袋有沿传送带下滑的趋势，所以米袋受到沿传送带向上的摩擦力，由于
，米袋做匀减速直线运动，根据牛顿第二定律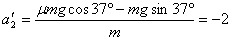
m/s2
根据位移公式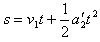
解方程得t=1s
本题解析：
本题难度：困难
4、实验题 光电计时器是一种研究物体运动情况的常见仪器。当有物体从光电门通过时，光电计时器就可以显示物体的挡光时间。现利用如图甲所示装置探究物体的加速度与合外力、质量的关系’其中NQ是水平桌面，PQ是一端带有滑轮的长木板，1、2是固定在木板上的两个光电门（与之连接的两个光电计时器没有画出）。小车上固定着用于挡光的窄片K，测得其宽度为d.小车从木板的顶端滑下’光电门各自连接的计时器显示窄片K的挡光时间分别为t1和t2。
(1) 该实验中，在改变小车的质量M或沙桶的总质量m时，应保持M?m,这样做的目的__
(2) 为了计算出小车的加速度，除了测量d、t1和t2之外，还需要测__________
若上述测量的量用x表示，则用这些叙理量计算加速度的表达式为a=__________
(3) 某位同学经过测量、计算得到如下表数据，请在图乙中作出小车加速度与所受合外力的关系图像。
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| M/kg | 0.58 | 0.58 | 0.58 | 0.58 | 0.58 | 0.58 | 0.58 |
| F/N | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 |
| a/m.s-2 | 0.13 | 0.17 | 0.26 | 0,34 | 0.43 | 0.51 | 0.59 |
参考答案：（1）小车所受合外力大小等于(或约等于)mg （2分）
（2）两光电门之间的距离（或“小车由光电门1运动至光电门2所用时间”） （2分） 
?（或“
”） （2分）
（3）如图?（2分）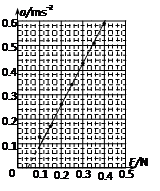
（4）木板倾角偏小（或“平衡摩擦力不足”或“末完全平衡摩擦力”） （2分）
本题解析：：（1）实验中我们认为：mg=Ma，而实际上是：mg=（M+m）a，因此只有当M＞＞m时，小车所受合外力大小等于mg．
故答案为：小车所受合外力大小等于（或约等于）mg．
（2）通过光电门的测量我们计算出了通过光电门1的速度为：v1=
，通过2时的速度为：v2=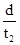
如果测量出经过1、2时的时间t，根据：a=
，得：a=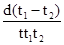
如果测出经过1、2时的距离x，根据：
=2ax，得：a=．
（3）如图?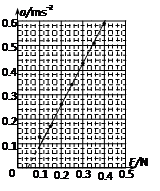
（4）由图乙可知，开始小车受合外力时，加速度却为零，因此操作过程中可能没有平衡摩擦力或者平衡摩擦力不足．
本题难度：一般
5、简答题 如图所示，AC、BC为位于竖直平面内的两根光滑细杆，A、B、C三点恰位于同一圆周上，C为该圆周的最低点，a、b为套在细杆上的两个小环，当两环同时从A、B点自静止开始下滑，则 （ ）
A．a环将先到达C点
B．b环将先到达C点
C．a、b环同时到达C点
D．由于两杆的倾角不知道，无法判断两环到达c点的先后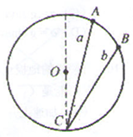
参考答案：小环在杆上做初速度为0的匀加速直线运动，如图，∠ACD=θ，小环在杆上下滑时的加速度a=gcosθ，令圆的半径为R，则根据几何关系有：
AC=2Rcosθ
小环在AC上下滑的加速度a=gcosθ，因为小环做初速度为0的匀加速直线运动，根据位移时间关系有：
AC=12at2
即2Rcosθ=12gcosθt2，
解得：t=
本题解析：
本题难度：一般