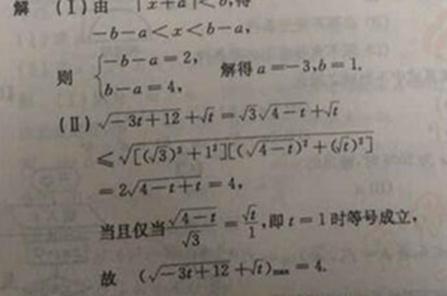时间:2015-06-15 07:11:37
21、(本小题满分12分)
设![]()
(I) 求![]() ;
;
(II) 证明:![]() 在(0,
在(0,![]() )内有且仅有一个零点(记为
)内有且仅有一个零点(记为![]() ),且0<
),且0<![]() -
-![]() <
<![]()
 .
.
考生注意:请在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分,作答时用2B铅笔在答题卡上把所选题目的题号后的方框涂黑.
22、(本小题满分10分)选修4-1:几何证明选讲
如图,AB切于![]() 于点B,直线AO交
于点B,直线AO交![]() 于D,E两点,BC
于D,E两点,BC![]() DE,垂足为C.
DE,垂足为C.

(I) 证明:![]() ;
;
(II) 若AD=3DC,BC=![]() ,求
,求![]() 的直径.
的直径.
23、(本小题满分10分)选修4-1,坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为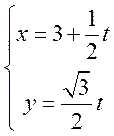 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I) 写出![]() 的直角坐标方程;
的直角坐标方程;
(II) P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
24、(本小题满分10分)选修4-5,不等式选讲
已知关于x的不等式|x+a|<b的解集为![]() .
.
(I) 求实数a,b的值.
(II) 求![]() +
+![]() 的最大值.
的最大值.
1![]()
2![]()
3![]()
4![]()
5![]()
6![]()
7![]()
8![]()
9![]()
10![]()
11![]()
12![]()
13、5
14.8
15.
16.
17.(I)因为![]() ,所以
,所以![]()
由正弦定理,得![]() ,
,
又![]() ,从而
,从而![]() ,
,
由于![]()
所以
(II)解法一:由余弦定理,得
![]() ,而
,而![]() ,
, ,
,
得![]() ,即
,即![]()
因为![]() ,所以
,所以![]() ,
,
故![]() 面积为
面积为 .
.
解法二:由正弦定理,得
从而
又由![]() 知
知![]() ,所以
,所以
故
 ,
,
所以![]() 面积为
面积为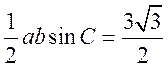 .
.
18.
(II)由已知,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]()
又由(I)知,![]() ,所以
,所以
![]() 平面
平面![]() ,
,
即![]() 是四棱锥
是四棱锥![]() 的高,
的高,
由图1可知,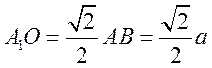 ,平行四边形
,平行四边形![]() 面积
面积![]() ,
,
从而四棱锥![]() 的为
的为
 ,
,
由 ,得
,得![]() .
.
19 (I)在容量为30的样本中,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率是![]() .
.
(II)称相邻两个日期为“互邻日期对”(如1日与2日,2日与3日等)这样在4月份中,前一天为晴天的互邻日期对有16对,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为![]() ,
,
以频率估计概率,运动会期间不下雨的概率为![]() .
.
考点:概率与统计.
20. (I)由题意知 ,
,
综合![]() ,解得
,解得![]() ,
,
所以,椭圆的方程为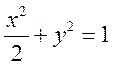 .
.
(II)由题设知,直线![]() 的方程为
的方程为![]() ,代入
,代入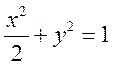 ,得
,得
![]() ,
,
由已知![]() ,设
,设![]() ,
,![]()
则 ,
,
从而直线![]() 与
与![]() 的斜率之和
的斜率之和

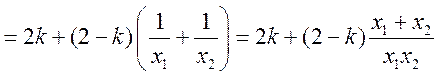
 .
.
21. (I)由题设![]() ,
,
所以![]() ①
①
由 ![]() ②
②
①![]() ②得
②得![]()
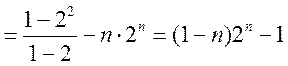 ,
,
所以 ![]()
(II)因为![]()
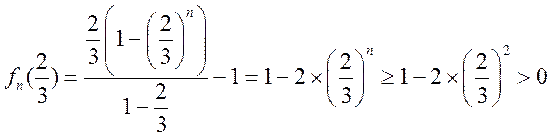 ,
,
所以![]() 在
在 内至少存在一个零点,
内至少存在一个零点,
又![]()
所以![]() 在
在 内单调递增,
内单调递增,
因此,![]() 在
在 内有且只有一个零点
内有且只有一个零点![]() ,
,
由于 ,
,
所以
由此可得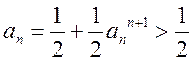
故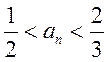
所以
22. (I)因为![]() 是
是![]() 的直径,
的直径,
则![]()
又![]() ,所以
,所以![]()
又![]() 切
切![]() 于点
于点![]() ,
,
得![]()
所以![]()
(II)由(I)知![]() 平分
平分![]() ,
,
则 ,
,
又![]() ,从而
,从而![]() ,
,
所以![]()
所以![]() ,
,
由切割线定理得![]()
即 ,
,
故![]() ,
,
即![]() 的直径为3.
的直径为3.
考点:1.几何证明;2.切割线定理.
23. (I)由![]() ,
,
得![]() ,
,
从而有![]()
所以
(II)设 ,又
,又![]() ,
,
则 ,
,
故当![]() 时,
时,![]() 取得最小值,
取得最小值,
此时![]() 点的坐标为
点的坐标为![]() .
.
考点:1. 坐标系与参数方程;2.点与圆的位置关系.
24. (I)由![]() ,得
,得![]()
则 ,解得
,解得![]()
(II)![]()
![]()
![]()
当且仅当 即
即![]() 时等号成立,
时等号成立,
故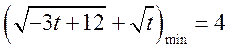
15、

16、
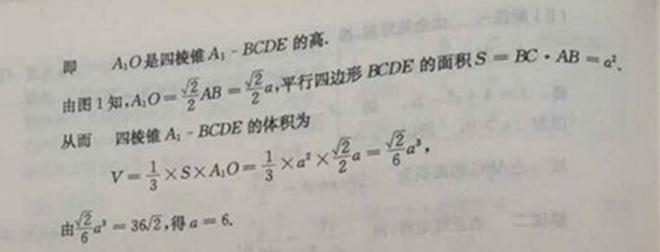
17、
18、

19、
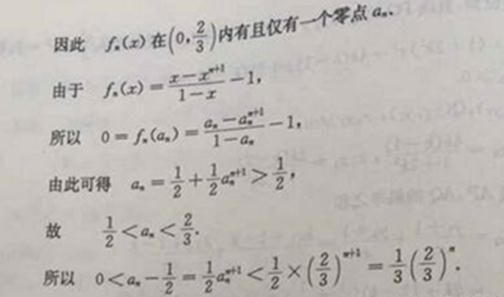
20、
21、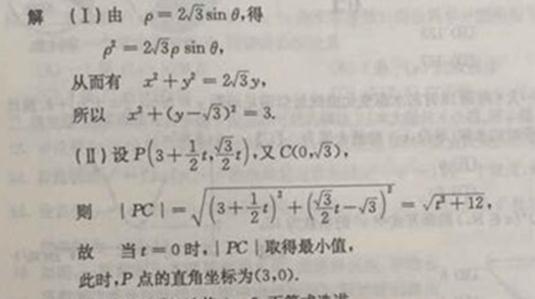
22、