时间:2015-06-10 21:58:10
2015年北京高考数学(理科)
本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.
第一部分(选择题共40分)
一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.复数![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若![]() ,
,![]() 满足
满足 则
则![]() 的最大值为
的最大值为
A.0 B.1 C.![]() D.2
D.2
3.执行如图所示的程序框图,输出的结果为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

4.设![]() ,
,![]() 是两个不同的平面,
是两个不同的平面,![]() 是直线且
是直线且![]() .“
.“![]() ”是“
”是“![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.某三棱锥的三视图如图所示,则该三棱锥的表面积是
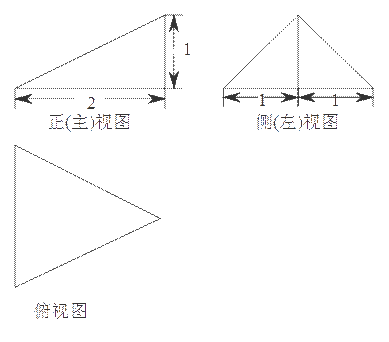
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
6.设![]() 是等差数列. 下列结论中正确的是
是等差数列. 下列结论中正确的是
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
7.如图,函数![]() 的图象为折线
的图象为折线![]() ,则不等式
,则不等式![]() 的解集是
的解集是
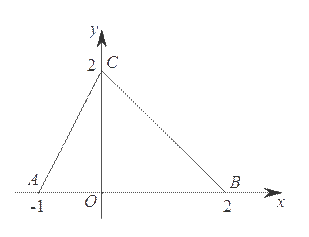
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是
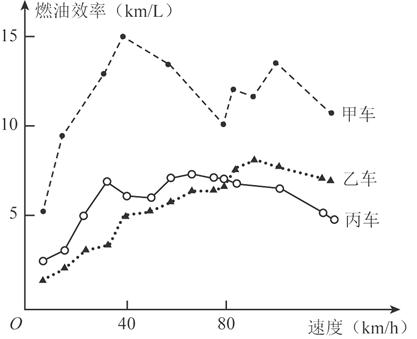
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
第二部分(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分.
9.在![]() 的展开式中,
的展开式中,![]() 的系数为 .(用数字作答)
的系数为 .(用数字作答)
10.已知双曲线 的一条渐近线为
的一条渐近线为![]() ,则
,则![]() .
.
11.在极坐标系中,点 到直线
到直线![]() 的距离为 .
的距离为 .
12.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则 .
.
13.在![]() 中,点
中,点![]() ,
,![]() 满足
满足![]() ,
,![]() .若
.若![]() ,则
,则![]() ;
;![]() .
.
14.设函数
①若![]() ,则
,则![]() 的最小值为 ;
的最小值为 ;
②若![]() 恰有2个零点,则实数
恰有2个零点,则实数![]() 的取值范围是 .
的取值范围是 .
三、解答题(共6小题,共80分.解答应写出文字说明,演算步骤或证明过程)
15.(本小题13分)
已知函数 .
.
(Ⅰ) 求![]() 的最小正周期;
的最小正周期;
(Ⅱ) 求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
16.(本小题13分)
![]() ,
,![]() 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,![]()
假设所有病人的康复时间互相独立,从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙.
组选出的人记为乙.
(Ⅰ) 求甲的康复时间不少于14天的概率;
(Ⅱ) 如果![]() ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ) 当![]() 为何值时,
为何值时,![]() ,
,![]() 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
17.(本小题14分)
如图,在四棱锥![]() 中,
中,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求二面角![]() 的余弦值;
的余弦值;
(Ⅲ) 若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.

18.(本小题13分)
已知函数 .
.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求证:当![]() 时,
时, ;
;
(Ⅲ)设实数![]() 使得
使得 对
对![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
19.(本小题14分)
已知椭圆![]() :
: 的离心率为
的离心率为![]() ,点
,点![]() 和点
和点![]()
![]() 都在椭
都在椭