时间:2015-05-02 20:28:28
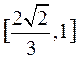
24.执行如图的程序框图,如果输入的t∈[-1,3],则输出的s属于
(A)[-3,4] (B)[-5,2] (C)[-4,3] (D)[-2,5]
25.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有
(A)36个 (B)24个 (C)18个 (D)6个
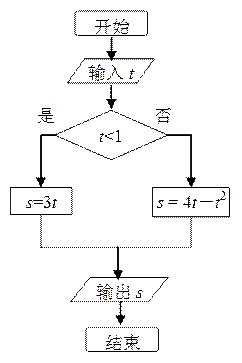
26.对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如下图所示),则该样本的中位数、众数、极差分别是
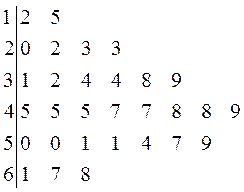
(A)46,45,56 (B)46,45,53
(C)47,45,56 (D)45,47,53
27.甲、乙两名射击运动员在某次测试中各射击20次,两人的测试成绩如下表:
|
甲的成绩 |
|
乙的成绩 | ||||||||
|
环数 |
7 |
8 |
9 |
10 |
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
频数 |
4 |
6 |
6 |
4 |
![]() ,
,![]() 分别表示甲、乙两名运动员这次测试成绩的标准差,
分别表示甲、乙两名运动员这次测试成绩的标准差,![]() ,
,![]() 分别表示甲、乙两名运动员这次测试成绩的平均数,则有
分别表示甲、乙两名运动员这次测试成绩的平均数,则有
(A)![]()
![]() ,
,![]()
![]() (B)
(B)![]()
![]() ,
,![]()
![]()
(C)![]()
![]() ,
,![]()
![]() (D)
(D)![]()
![]() ,
,![]()
![]()
28.从![]() 中随机选取一个数为
中随机选取一个数为![]() ,从
,从![]() 中随机选取一个数为
中随机选取一个数为![]() ,则
,则![]() 的概率是
的概率是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
29.节日前夕,小李在家门前的树上挂了两串彩灯. 这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮. 那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是
(A) ![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
二、填空题:直接填写结果,不必写出具体解答过程.
1.![]() 的值是________.
的值是________.
2.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x. 那么,不等式f(x+2)<5的解集是__________.
 3.设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=______.
3.设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=______.
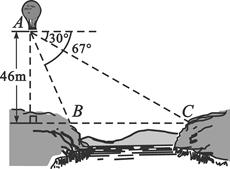
4.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于_______m.
(用四舍五入法将结果精确到个位.参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() )
)
5.设![]() 的内角
的内角![]() 所对边的长分别为
所对边的长分别为![]() .若
.若![]() ,
,![]() 则角
则角![]() _________.
_________.
6.等差数列{an}的前n项和为Sn ,已知S10=0,S15 =25,则nSn 的最小值为________.
7.已知函数f(x)=4x+![]() (x>0,a>0)在x=3时取得最小值,则a=___________.
(x>0,a>0)在x=3时取得最小值,则a=___________.
8.设D,E分别是DABC的边AB,BC上的点,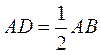 ,
,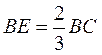 ,若
,若![]()
![]() (
(![]() 为实数),则
为实数),则![]() 的值为 ________.
的值为 ________.
9.椭圆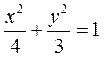 的左焦点为
的左焦点为![]() ,直线
,直线![]() 与椭圆交于点
与椭圆交于点![]() 、
、![]() .当△
.当△![]() 的周长最大时,△
的周长最大时,△![]() 的面积是 .
的面积是 .
10.设![]() ,过定点A的动直线
,过定点A的动直线![]() 和过定点B的动直线
和过定点B的动直线![]() 交于点
交于点![]() ,则
,则![]() 的最大值是_______.
的最大值是_______.
11.某几何体的三视图如图所示,则该几何体的体积为______.
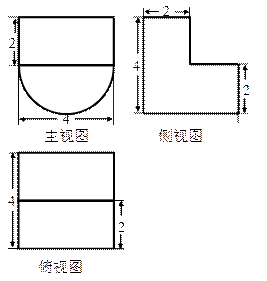
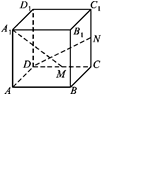 12.如图所示,在正方体
12.如图所示,在正方体![]() 中,M、N分别是棱CD、
中,M、N分别是棱CD、![]() 的中点,则异面直线
的中点,则异面直线![]() 与DN所成的角的大小是 .
与DN所成的角的大小是 .
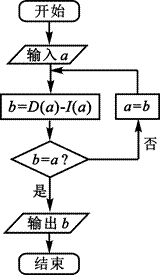
13.设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为![]() ,按从大到小排成的三位数记为
,按从大到小排成的三位数记为![]() (例如
(例如![]() ,则
,则![]() ,
,![]() ).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果
).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果![]() ________.
________.
14.已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=______.
|
|
15.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图.由图中数据可知![]() .若要从身高在[ 120 , 130),[130 ,140), [140, 150]三组内的学生中,用分层抽样方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
.若要从身高在[ 120 , 130),[130 ,140), [140, 150]三组内的学生中,用分层抽样方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为 .
16.设P1,P2,…,Pn为平面a内的n个点,在平面a内的所有点中,若点P到点P1,P2,…,Pn的距离之和最小,则称点P为点P1,P2,…,Pn的一个“中位点”.例如,线段AB上的任意点都是端点A,B的中位点.现有下列命题:
① 若三个点A,B,C共线,C在线段AB上,则C是A,B,C的中位点;
② 直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③ 若四个点A,B,C,D共线,则它们的中位点存在且唯一;
④ 梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是__________.(写出所有真命题的序号)
17.以![]() 表示值域为
表示值域为![]() 的函数组成的集合,
的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数M,使得函数
,存在一个正数M,使得函数![]() 的值域包含于区间
的值域包含于区间![]() .例如,当
.例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() .现有如下命题:
.现有如下命题:
① 设函数![]() 的定义域为D,则“
的定义域为D,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”;
”;
② 函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值;
有最大值和最小值;
③ 若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,则
,则![]() ;
;
④ 若函数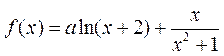 (
(![]() ,
,![]() )有最大值,则
)有最大值,则![]() .
.
其中的真命题有_______.(写出所有真命题的序号)
三、解答题:解答应写出必要的文字说明、演算步骤或证明过程.
1.在等差数列![]() 中,
中,![]() ,且
,且![]() 为
为![]() 和
和![]() 的等比中项,求数列
的等比中项,求数列![]() 的首项、公差及前
的首项、公差及前![]() 项和.
项和.
2.已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ) 证明:![]() ;
;
(Ⅱ) 是否存在![]() ,使得
,使得![]() 为等差数列?并说明理由.
为等差数列?并说明理由.
3.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(Ⅰ) 若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,![]() )的函数解析式;
)的函数解析式;