2016考研数学（一）真题完整版

一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸指定位置上.

（1）若反常积分收敛，则（    ）

（2）已知函数，则的一个原函数是（    ）

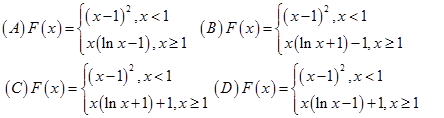
（3）若是微分方程的两个解，则（   ）

（4）已知函数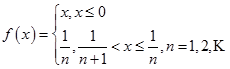，则（     ）

（A）是的第一类间断点   （B）是的第二类间断点

（C）在处连续但不可导    （D）在处可导

（5）设A，B是可逆矩阵，且A与B相似，则下列结论错误的是（    ）

（A）与相似         （B）与相似     

（C）与相似  （D）与相似

（6）设二次型，则在空间直角坐标下表示的二次曲面为（   ）

（A）单叶双曲面    （B）双叶双曲面   （C）椭球面    （C）柱面

 

（7）设随机变量，记，则（    ）

（A）随着的增加而增加             （B）随着的增加而增加

（C）随着的增加而减少             （D）随着的增加而减少

（8）随机试验有三种两两不相容的结果，且三种结果发生的概率均为，将试验独立重复做2次，表示2次试验中结果发生的次数，表示2次试验中结果发生的次数，则与的相关系数为（    ）

 

二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.

（9）

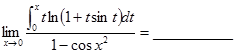
（10）向量场的旋度

（11）设函数可微，由方程确定，则

（12）设函数，且，则

（13）行列式____________.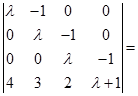

（14）设为来自总体的简单随机样本，样本均值，参数的置信度为0.95的双侧置信区间的置信上限为10.8，则的置信度为0.95的双侧置信区间为______.

三、解答题：15—23小题，共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.

（15）（本题满分10分）已知平面区域，计算二重积分.

（16）（本题满分10分）设函数满足方程其中.

证明：反常积分收敛；

若求的值.

 

（17）（本题满分10分）设函数满足且是从点到点的光滑曲线，计算曲线积分，并求的最小值

（18）设有界区域由平面与三个坐标平面围成，为整个表面的外侧，计算曲面积分

（19）（本题满分10分）已知函数可导，且，，设数列满足，证明：

（I）级数绝对收敛；

（II）存在，且.

（20）（本题满分11分）设矩阵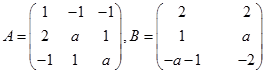

当为何值时，方程无解、有唯一解、有无穷多解？

（21）（本题满分11分）已知矩阵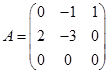

（I）求

（II）设3阶矩阵满足，记将分别表示为的线性组合。

（22）（本题满分11分）设二维随机变量在区域上服从均匀分布，令

（I）写出的概率密度；

（II）问与是否相互独立？并说明理由；

（III）求的分布函数.

（23）设总体的概率密度为，其中为未知参数，为来自总体的简单随机样本，令。

（1）求的概率密度

（2）确定，使得为的无偏估计

 

 ★ 考研信息汇总 ★   ★ 考研历年真题 ★   ★ 考研经验技巧汇总 ★