时间:2016-03-06 19:05:35
(II)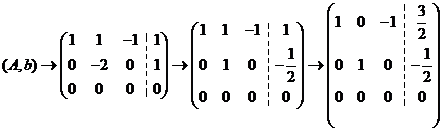
原方程组等价为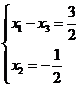 ,即
,即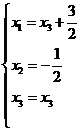 ,
,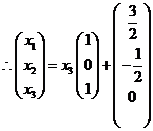 。
。
![]() 的通解为
的通解为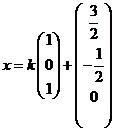 ,
,![]() 为任意常数。
为任意常数。
(21) (本题满分11 分)
已知二次型![]() 在正交变换
在正交变换![]() 下的标准型为
下的标准型为![]() ,且
,且![]() 的第3列为
的第3列为![]() .
.
(I) 求矩阵![]() ;
;
(II) 证明![]() 为正定矩阵,其中
为正定矩阵,其中![]() 为3阶单位矩阵
为3阶单位矩阵
【考点】实对称矩阵的特征值和特征向量的性质,二次型的标准形的概念,正定矩阵的判别法
【详解】本题涉及到的主要知识点
含有n个变量![]() 的二次齐次多项式
的二次齐次多项式
![]()
称为n元二次型。令![]() ,
,![]() ,则二次型可用矩阵乘法表示为
,则二次型可用矩阵乘法表示为
![]() ,
,
其中A是n阶实对称矩阵(![]() ),称A为二次型
),称A为二次型![]() 的矩阵,矩阵A的秩r(A)称为二次型的秩。
的矩阵,矩阵A的秩r(A)称为二次型的秩。
如果二次型中只含有变量的平方项,所有混合项的系数全是零,则成为标准型。
对二次型![]() ,如对任何x不为0,恒有
,如对任何x不为0,恒有![]() >0,则称二次型为正定二次型。
>0,则称二次型为正定二次型。
在本题中,
(1)由于二次型在正交变换![]() 下的标准形为
下的标准形为![]() ,所以
,所以![]() 的特征值为
的特征值为![]() 。
。
由于![]() 的第3列为
的第3列为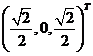 ,所以
,所以![]() 对应于
对应于![]() 的特征向量为
的特征向量为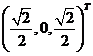 ,记
,记![]() 。
。
由于![]() 是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于
是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于![]() 的特征向量为
的特征向量为![]() ,则
,则![]() ,即
,即![]() 。取
。取
![]() ,
,
则![]() 为对应于
为对应于![]() 的特征向量。
的特征向量。
方法一:由![]() ,两边取转置,得
,两边取转置,得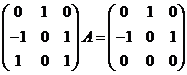 。
。
解此矩阵方程:

所以,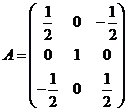 。
。
方法二:
由于![]() 是相互正交的,所以只需单位化:
是相互正交的,所以只需单位化:
![]() 。
。
取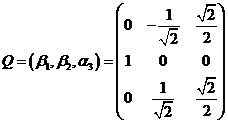 ,则
,则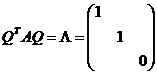 ,
,
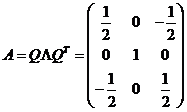 。
。
(II)![]() 也是实对称矩阵,
也是实对称矩阵,![]() 的特征值为1,1,0,所以
的特征值为1,1,0,所以![]() 的特征值为2,2,1,由于
的特征值为2,2,1,由于![]() 的特征值全大于零,故
的特征值全大于零,故![]() 是正定矩阵。
是正定矩阵。
(22) (本题满分11 分)
设二维随机变量![]() 的概率密度为
的概率密度为
![]() ,
,![]() ,
,![]() ,
,
求常数![]() 及条件概率密度
及条件概率密度![]()
【考点】二维连续型随机变量的条件密度,二维正态分布的概率密度
【详解】本题涉及到的主要知识点
连续型随机变量的条件概率分布:
(1)设(X,Y)~f(x,y),若对于固定的y,边缘概率密度![]() ,则称
,则称![]() 为在Y=y的条件下的X的条件概率密度,记为
为在Y=y的条件下的X的条件概率密度,记为![]() 。
。
(2)同样,设![]() ,则称
,则称![]() 为在X=x的条件下的Y的条件概率密度,记为
为在X=x的条件下的Y的条件概率密度,记为
![]() 。
。
二维正态分布的概念:
如果二维连续型随机变量(X,Y)的联合概率密度为
![]()
则称(X,Y)服从参数为![]() 的二维正态分布,记为(X,Y)~N(
的二维正态分布,记为(X,Y)~N(![]() ).其中
).其中![]() 均为常数且
均为常数且![]() 。
。
在本题中,
![]()
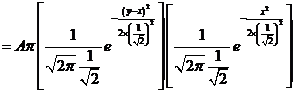
利用概率密度的性质得到
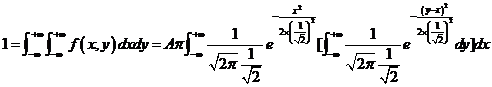
因为,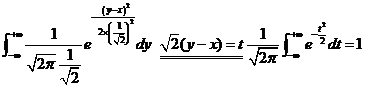 ;
;
同理,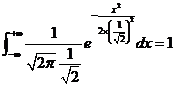 ,所以
,所以
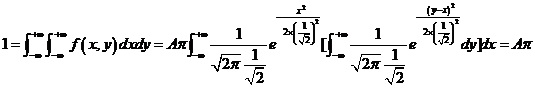
(利用正态分布的概率密度为1,即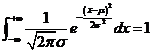 ),得到
),得到![]()
即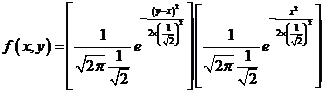
![]() 的边缘概率密度为
的边缘概率密度为
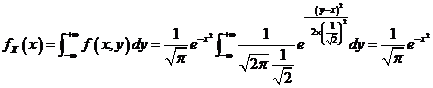
条件概率密度
![]()
(23) (本题满分11分)
设总体![]() 的概率分布为
的概率分布为
|
|
1 |
2 |
3 |
|
|
|
|
|
其中![]() 未知,以
未知,以![]() 表示来自总体
表示来自总体![]() 的简单随机样本(样本容量为
的简单随机样本(样本容量为![]() )中等于
)中等于![]() 的个数(
的个数(![]() ).试求常数
).试求常数![]() ,使
,使![]() 为
为![]() 的无偏估计量,并求
的无偏估计量,并求![]() 的方差.
的方差.
【考点】常用抽样分布,估计量的无偏性
【详解】本题涉及到的主要知识点
对于总体X的n次独立重复观测,称为来自总体X的n此简单随机抽样。
随机变量数学期望的性质:![]()
方差的定义及性质:设X是一个随机变量,若![]() 存在,则称
存在,则称![]() 为X的方差,记为D(X)。若X和Y相互独立,则
为X的方差,记为D(X)。若X和Y相互独立,则![]() .
.
在此题中,
![]()
![]()
![]()
![]()
因为![]() 是
是![]() 的无偏估计量,所以
的无偏估计量,所以![]() 即得
即得
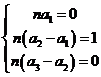
整理得到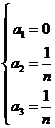
所以统计量![]()
![]()