时间:2016-03-06 15:36:39
![]()
所以, ![]() ,
,
![]() ,
,
![]()
![]()
=![]()
(或![]() ),
),
故(X,Y)的概率分布为
![]()
![]() Y
Y
X 0 1
![]() 0
0 ![]()
![]()
1 ![]()
![]()
(II) X, Y的概率分布分别为
![]()
![]() X 0 1 Y 0 1
X 0 1 Y 0 1
![]()
![]() P
P ![]()
![]() P
P ![]()
![]()
则![]() ,
,![]() ,DY=
,DY=![]() , E(XY)=
, E(XY)=![]() ,
,
故 ![]() ,从而
,从而
![]()
【评注】 本题尽管难度不大,但考察的知识点很多,综合性较强。通过随机事件定义随机变量或通过随机变量定义随机事件,可以比较好地将概率论的知识前后连贯起来,这种命题方式值得注意。
原题见《考研数学大串讲》P274例3.
(23)(本题满分9分)
设总体X的分布函数为
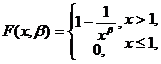
其中未知参数![]() 为来自总体X的简单随机样本,求:
为来自总体X的简单随机样本,求:
(I) ![]() 的矩估计量;
的矩估计量;
(II) ![]() 的最大似然估计量.
的最大似然估计量.
【分析】 先由分布函数求出概率密度,再根据求矩估计量和最大似然估计量的标准方法进行讨论即可。
【详解】 X的概率密度为
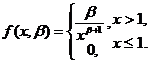
(I) 由于
![]() ,
,
令![]() ,解得
,解得 ![]() ,所以参数
,所以参数![]() 的矩估计量为
的矩估计量为
![]()
(II)似然函数为
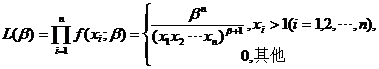
当![]() 时,
时,![]() ,取对数得
,取对数得
![]() ,
,
两边对![]() 求导,得
求导,得
![]() ,
,
令![]() ,可得
,可得 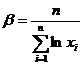 ,
,
故![]() 的最大似然估计量为
的最大似然估计量为
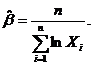
【评注】 本题是基础题型,难度不大,但计算量比较大,实际做题时应特别注意计算的准确性。
完全类似的例题见《数学复习指南》P596例6.9, 《数学题型集粹与练习题集》P364第十三题,《数学一临考演习》P26第23题.