时间:2016-03-06 13:30:15
【评注】 本题属基本题型.
二、选择题(本题共6小题,每小题4分,满分24分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(1)设函数f(x)在![]() 内连续,其导函数的图形如图所示,则f(x)有
内连续,其导函数的图形如图所示,则f(x)有
(A) 一个极小值点和两个极大值点.
(B) 两个极小值点和一个极大值点.
(C) 两个极小值点和两个极大值点.
(D) 三个极小值点和一个极大值点. [ C ]
![]() y
y


![]() O x
O x
【分析】 答案与极值点个数有关,而可能的极值点应是导数为零或导数不存在的点,共4个,是极大值点还是极小值可进一步由取极值的第一或第二充分条件判定.
【详解】 根据导函数的图形可知,一阶导数为零的点有3个,而 x=0 则是导数不存在的点. 三个一阶导数为零的点左右两侧导数符号不一致,必为极值点,且两个极小值点,一个极大值点;在x=0左侧一阶导数为正,右侧一阶导数为负,可见x=0为极大值点,故f(x)共有两个极小值点和两个极大值点,应选(C).
【评注】 本题属新题型,类似考题2001年数学一、二中曾出现过,当时考查的是已知f(x)的图象去推导![]() 的图象,本题是其逆问题. 完全类似例题在文登学校经济类串讲班上介绍过.
的图象,本题是其逆问题. 完全类似例题在文登学校经济类串讲班上介绍过.
(2)设![]() 均为非负数列,且
均为非负数列,且![]() ,
,![]() ,
,![]() ,则必有
,则必有
(A) ![]() 对任意n成立. (B)
对任意n成立. (B) ![]() 对任意n成立.
对任意n成立.
(C) 极限![]() 不存在. (D) 极限
不存在. (D) 极限![]() 不存在. [ D ]
不存在. [ D ]
【分析】 本题考查极限概念,极限值与数列前面有限项的大小无关,可立即排除(A),(B); 而极限![]() 是
是![]() 型未定式,可能存在也可能不存在,举反例说明即可;极限
型未定式,可能存在也可能不存在,举反例说明即可;极限![]() 属
属![]() 型,必为无穷大量,即不存在.
型,必为无穷大量,即不存在.
【详解】 用举反例法,取![]() ,
,![]() ,
,![]() ,则可立即排除(A),(B),(C),因此正确选项为(D).
,则可立即排除(A),(B),(C),因此正确选项为(D).
【评注】 对于不便直接证明的问题,经常可考虑用反例,通过排除法找到正确选项. 完全类似方法见《数学最后冲刺》P.179.
(3)已知函数f(x,y)在点(0,0)的某个邻域内连续,且![]() ,则
,则
(A) 点(0,0)不是f(x,y)的极值点.
(B) 点(0,0)是f(x,y)的极大值点.
(C) 点(0,0)是f(x,y)的极小值点.
(D) 根据所给条件无法判断点(0,0)是否为f(x,y)的极值点. [ A ]
【分析】 由题设,容易推知f(0,0)=0,因此点(0,0)是否为f(x,y)的极值,关键看在点(0,0)的充分小的邻域内f(x,y)是恒大于零、恒小于零还是变号.
【详解】 由 ![]() 知,分子的极限必为零,从而有f(0,0)=0, 且
知,分子的极限必为零,从而有f(0,0)=0, 且
![]()
![]() 充分小时),于是
充分小时),于是
![]()
可见当y=x且![]() 充分小时,
充分小时,![]() ;而当y= -x且
;而当y= -x且![]() 充分小时,
充分小时,![]() . 故点(0,0)不是f(x,y)的极值点,应选(A).
. 故点(0,0)不是f(x,y)的极值点,应选(A).
【评注】 本题综合考查了多元函数的极限、连续和多元函数的极值概念,题型比较新,有一定难度. 将极限表示式转化为极限值加无穷小量,是有关极限分析过程中常用的思想。
(4)设向量组I:![]() 可由向量组II:
可由向量组II:![]() 线性表示,则
线性表示,则
(A) 当![]() 时,向量组II必线性相关. (B) 当
时,向量组II必线性相关. (B) 当![]() 时,向量组II必线性相关.
时,向量组II必线性相关.
(C) 当![]() 时,向量组I必线性相关. (D) 当
时,向量组I必线性相关. (D) 当![]() 时,向量组I必线性相关.
时,向量组I必线性相关.
[ D ]
【分析】 本题为一般教材上均有的比较两组向量个数的定理:若向量组I:![]() 可由向量组II:
可由向量组II:![]() 线性表示,则当
线性表示,则当![]() 时,向量组I必线性相关. 或其逆否命题:若向量组I:
时,向量组I必线性相关. 或其逆否命题:若向量组I:![]() 可由向量组II:
可由向量组II:![]() 线性表示,且向量组I线性无关,则必有
线性表示,且向量组I线性无关,则必有![]() . 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
. 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
【详解】 用排除法:如![]() ,则
,则![]() ,但
,但![]() 线性无关,排除(A);
线性无关,排除(A);![]() ,则
,则![]() 可由
可由![]() 线性表示,但
线性表示,但![]() 线性无关,排除(B);
线性无关,排除(B);![]() ,
,![]() 可由
可由![]() 线性表示,但
线性表示,但![]() 线性无关,排除(C). 故正确选项为(D).
线性无关,排除(C). 故正确选项为(D).
【评注】 本题将一已知定理改造成选择题,如果考生熟知此定理应该可直接找到答案,若记不清楚,也可通过构造适当的反例找到正确选项。
(5)设有齐次线性方程组Ax=0和Bx=0, 其中A,B均为![]() 矩阵,现有4个命题:
矩阵,现有4个命题:
① 若Ax=0的解均是Bx=0的解,则秩(A)![]() 秩(B);
秩(B);
② 若秩(A)![]() 秩(B),则Ax=0的解均是Bx=0的解;
秩(B),则Ax=0的解均是Bx=0的解;
③ 若Ax=0与Bx=0同解,则秩(A)=秩(B);
④ 若秩(A)=秩(B), 则Ax=0与Bx=0同解.
以上命题中正确的是
(A) ① ②. (B) ① ③.
(C) ② ④. (D) ③ ④. [ B ]
【分析】 本题也可找反例用排除法进行分析,但① ②两个命题的反例比较复杂一些,关键是抓住③ 与 ④,迅速排除不正确的选项.
【详解】 若Ax=0与Bx=0同解,则n-秩(A)=n - 秩(B), 即秩(A)=秩(B),命题③成立,可排除(A),(C);但反过来,若秩(A)=秩(B), 则不能推出Ax=0与Bx=0同解,如![]() ,
,![]() ,则秩(A)=秩(B)=1,但Ax=0与Bx=0不同解,可见命题④不成立,排除(D),故正确选项为(B).
,则秩(A)=秩(B)=1,但Ax=0与Bx=0不同解,可见命题④不成立,排除(D),故正确选项为(B).
【例】 齐次线性方程组Ax=0与Bx=0同解的充要条件
(A) r(A)=r(B). (B) A,B为相似矩阵.
(C) A, B的行向量组等价. (D) A,B的列向量组等价. [ C ]
有此例题为基础,相信考生能迅速找到答案.
(6)设随机变量![]() ,则
,则
(A) ![]() . (B)
. (B) ![]() .
.
(C) ![]() . (D)
. (D) ![]() . [ C ]
. [ C ]
【分析】 先由![]() 分布的定义知
分布的定义知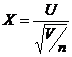 ,其中
,其中![]() ,再将其代入
,再将其代入![]() ,然后利用F分布的定义即可.
,然后利用F分布的定义即可.
【详解】 由题设知,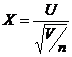 ,其中
,其中![]() ,于是
,于是
![]() =
=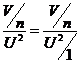 ,这里
,这里![]() ,根据F分布的定义知
,根据F分布的定义知![]() 故应选(C).
故应选(C).
【评注】 本题综合考查了t分布、![]() 分布和F分布的概念,要求熟练掌握此三类常用统计量分布的定义.
分布和F分布的概念,要求熟练掌握此三类常用统计量分布的定义.
三 、(本题满分10分)
过坐标原点作曲线y=lnx的切线,该切线与曲线y=lnx及x轴围成平面图形D.
(1) 求D的面积A;
(2) 求D绕直线x=e旋转一周所得旋转体的体积V.
【分析】 先求出切点坐标及切线方程,再用定