时间:2016-03-06 13:13:08
1999考研数一真题及答案解析
一、填空题(本题共5个小题，每小题3分，满分15分。把正确答案填写在题中横线上。)
(1) 
(2) 
(3) 
的通解为
(4) 设n 阶矩阵A 的元素全为1，则A 的
个特征值是
(5) 设两两相互独立的三事件A, B 和C 满足条件：
则
二、选择题(本题共5小题，每小题3分，满分15分。每小题给出得四个选项中，只有一个是符合题目要求的，把所选项前的字母填在提后的括号内。)
(1)设
是连续函数，
是的原函数，则 ( )
(A) 当是奇函数时，必是偶函数。
(B) 当是偶函数时，必是奇函数。
(C) 当是周期函数时，必是周期函数。
(D) 当是单调增函数时，必是单调增函数。
(2)设
其中
是有界函数，则在
处 ( )
(A)极限不存在 (B)极限存在，但不连续
(C)连续，但不可导 (D)可导
(3) 设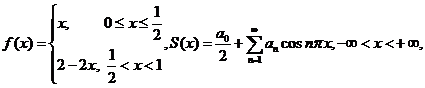
其中
则
等于 ( )
(A)
(B)
(C)
(D)
(4)设A 是
矩阵， B 是
矩阵，则
(A)当
时，必有行列式
(B)当时，必有行列式
(C)当
时，必有行列式 (D)当时，必有行列式
(5)设两个相互独立的随机变量X 和Y 分别服从正态分布N
和N
，则
(A) 
(B) 
(C) 
(D) 
三、(本题满分5分)
设
，
是由方程
和
=0所确定的函数，其中
和
分别具有一阶连续导数和一阶连续偏导数，求
。
四、(本题满分5分)
求
其中a,b 为正常数， L 为从点A
沿曲线
到点O
的弧.
五、 (本题满分6分)
设函数
二阶可导，且
，
.过曲线
上任意一点
作该曲线的切线及
轴的垂线，上述两直线与轴所围成的三角形的面积记为
，区间
上以为曲边的曲边梯形面积记为
，并设
恒为1，求此曲线的方程.
六、(本题满分6分)
试证：当
时，
七、(本题满分6分)
为清除井底的污泥，用缆绳将抓斗放入井底，抓起污泥后提出井口
见图，已知井深
30m,抓斗自重
, 缆绳每米重
，抓斗抓
起的污泥重
，提升速度为
,在提升过程中，污泥以
的速度从抓斗缝隙中漏掉，现将抓起污泥的抓斗提升至井口，问克服重
力需作多少焦耳的功？(说明：①
其中
分别表示
米，牛顿，秒，焦耳；②抓斗的高度及位于井口上方的缆绳长度忽略不
计.)
八、(本题满分7分)
设S 为椭球面
的上半部分，点P
∈S,π为S 在点P 处的切平面，
为点O
到平面π的距离，求
九、(本题满分7分)
设
(1) 求
的值；
(2) 试证：对任意的常数λ>0, 级数
收敛
十、(本题满分8分)
设矩阵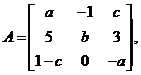
其行列式
又A 的伴随矩阵
有一个特征值
，属于的一个特征向量为
求
和的值.
十一、(本题满分6分)
设A 为m 阶实对称矩阵且正定，B为m×n实矩阵，
为B的转置矩阵，试证：
为正定矩阵的充分必要条件是B的秩
.
十二、(本题满分8分)
设随机变量X 与Y 相互独立，下表列出了二维随机变量
联合分布律及关于X 和关于Y 的边缘分布律中的部分数值，试将其余数值填入表中的空白处.
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
十三、(本题满分6分)
设总体X 的概率密度为
是取自总体X 的简单随机样本.
(1) 求θ的矩估计量
(2) 求的方差
1999 年全国硕士研究生入学统一考试数学一试题解析
一、填空题(本题共5个小题，每小题3分，满分15分.把正确答案填写在题中横线上.)
(1)【答案】
【分析】利用
的等价变换和洛必达法则求函数极限.
【详解】
方法1：
方法2：
(2)【答案】
【分析】欲求
，唯一的办法是作变换，使含有
中的“转移”到
之外
【详解】令
，则
，所以有
(3)【答案】
其中
为任意常数.
【分析】先求出对应齐次方程的通解，再求出原方程的一个特解.
【详解】原方程对应齐次方程
的特征方程为：
解得
，故的通解为
由于非齐次项为
因此原方程的特解可设为
代入原方程可求得
，故所求通解为
(4)【详解】因为
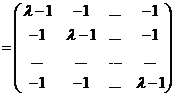(对应元素相减)
两边取行列式，
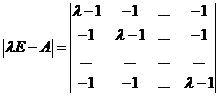
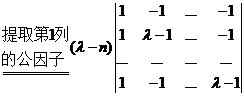
令
，得
，故矩阵A的n个特征值是n和0(
重)
(5)【答案】
【详解】根据加法公式有
因为
，设
由于
两两相互独立，所以有
，
，
，
又由于
，因此有
所以
又
，从而
，则有
，解得 
因
，故 
，即
二、选择题
(1)【答案】( A )
【详解】应用函数定义判定函数的奇偶性、周期性和单调性.
的原函数可以表示为
于是
当为奇函数时，
，从而有
即 F(x)为偶函数. 故(A)为正确选项.
(B)、(C)、(D)可分别举反例如下：
是偶函数，但其原函数
不是奇函数，可排除(B)；
是周期函数，但其原函数
不是周期函数，可排除(C)；
在区间
内是单调增函数，但其原函数
在区间内非单调增函数，可排除(D).
(2)【答案】( D )
【详解】由于可导必连续，连续则极限必存在，可以从函数可导性入手.
因为 
从而，
存在，且
，故正确选项为(D).
(3)【答案】( C )
【详解】由题设知，应先将从[0,1)作偶延拓，使之成为区间[−1,1]上的偶函数，然后再作周期(周期2)延拓，进一步展开为傅里叶级数，
而
是的间断点，按狄利克雷定理有，
(4)【答案】B
【详解】
方法1：
是矩阵，
是矩阵，则
是
阶方阵，因
.
当时，有
. (
的系数矩阵的秩小于未知数的个数)，故有行列式
，故应选(B).
方法2：是矩阵, 当时, 则
(系数矩阵的秩小于未知数的个数) ，方程组
必有非零解，即存在
，使得
，两边左乘，得
，即
有非零解，从而，故选(B).
方法3：用排除法
(A)，取
，，(A)不成立
(C)，取
，，(C)不成立
(D)，取
，
，(D)不成立，故选(B).
(5)【答案】B
【详解】 根据正态分布的性质：服从正态分布的独立随机变量的线性组合仍服从正态分布.
因
相互独立，且
，
，所以
, 
其中
，
，
，
由期望的性质：
，
由独立随机变量方差的性质：
所以 
，
(一般来说遇到正态分布的小题，主要就考两点，标准化和对称性，考虑问题也是从这两点出发)
A选项： 因
由标准化的定义：若
，则
所以，
，将其标准化有
(保证变换过程中概率不变，所以不等号的左边怎么变，右边也同样的变化)
又因为标准正态分布图像是关于
轴对称，所以
，而
，所以A错.
B选项：
将其标准化有：
(根据标准正态分布的对称性)
故B正确.
C选项：
将其标准化有：
，故C错.
D选项：
将其标准化有：
，故D错.
三【详解】分别在和
的两端对求导数，得
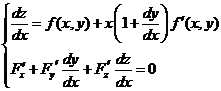
整理后得 
解此方程组，得
四【详解】
方法1：凑成闭合曲线，应用格林公式.
添加从点
沿
到点
的有向直
线段
, 如图，则
利用格林公式，前一积分
其中D为+L所围成的半圆域，后一积分选择为参数，得:
可直接积分 
，故 
方法2：将曲线积分分成两部分，其中一部分与路径无关，余下的积分利用曲线的参数方程计算.
前一积分与路径无关，所以
对后一积分，取
的参数方程
，则
，
从
到
，得
从而 
五【详解】如图，曲线上点
处的切线方程为
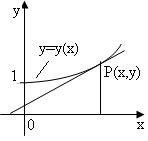所以切线与轴的交点为
由于
因此
于是 
又
，
根据题设
即 
两边对求导并化简得 
这是可降阶得二阶常微分方程，令
则
，
则上述方程可化为
分离变量得
，解得 
即
从而有 
，根据 
可得
故所求曲线得方程为 
六【详解】构造函数，利用函数的单调性，
证法1：令 
易知
又 
可见，当
时，
；当
时，
因此，
为
的最小值，即当
时，
，
