时间:2016-03-06 12:49:56
一、填空题(本题共5个小题,每小题3分,满分15分,把答案填在题中横线上.)
(1) 设
,则
___________.
(2) 设一平面经过原点及点(6,-3,2),且与平面
垂直,则此平面方程为
___________.
(3) 微分方程
的通解为___________.
(4) 函数
在
点处沿
点指向
点方向的方向导数为___________.
(5) 设是
矩阵,且的秩
,而
,则
___________.
二、选择题(本题共5个小题,每小题3分,满分15分.在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1) 已知
为某函数的全微分,则
等于 ( )
(A) -1 (B) 0 (C) 1 (D) 2
(2) 设
有二阶连续导数,且
,
,则 ( )
(A) 
是的极大值
(B) 是的极小值
(C) 
是曲线
的拐点
(D) 不是的极值,也不是曲线的拐点
(3) 设
,且
收敛,常数
,则级数
( )
(A) 绝对收敛 (B) 条件收敛 (C) 发散 (D) 收敛性与
有关
(4) 设有连续的导数,
,
,
,且当
时,
与
是同阶无穷小,则
等于 ( )
(A) 1 (B) 2 (C) 3 (D) 4
(5) 四阶行列式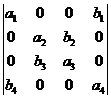
的值等于 ( )
(A) 
(B) 
(C) 
(D) 
三、(本题共2小题,每小题5分,满分10分.)
(1) 求心形线
的全长,其中
是常数.
(2) 设
,
,试证数列
极限存在,并求此极限.
四、(本题共2小题,每小题6分,满分12分.)
(1) 计算曲面积分
,其中
为有向曲面
,其法向量与
轴正向的夹角为锐角.
(2) 设变换
可把方程
化简为
,求常数,其中
有二阶连续的偏导数.
五、(本题满分7分)
求级数
的和.
六、(本题满分7分)
设对任意
,曲线上点
处的切线在
轴上的截距等于
,求的一般表达式.
七、(本题满分8分)
设在
上具有二阶导数,且满足条件
,
,其中
都是非负常数,
是(0,1)内任一点,证明
.
八、(本题满分6分)
设
,其中
是
阶单位矩阵,
是维非零列向量,
是的转置,证明：
(1) 
的充要条件是
；(2) 当时,是不可逆矩阵.
九、(本题满分8分)
已知二次型
的秩为2.
(1) 求参数及此二次型对应矩阵的特征值；
(2) 指出方程
表示何种二次曲面.
十、填空题(本题共2小题,每小题3分,满分6分.)
(1) 设工厂和工厂
的产品的次品率分别为1%和 2%,现从由和的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属生产的概率是__________.
(2) 设、
是两个相互独立且均服从正态分布
的随机变量,则随机变量
的数学期望
__________.
十一、(本题满分6分.)
设、是相互独立且服从同一分布的两个随机变量,已知的分布律为
,
=1,2,3,又设
,
.
(1) 写出二维随机变量
的分布律：
|
|
1 |
2 |
3 |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
(2) 求随机变量
的数学期望
.
一、填空题(本题共5个小题,每小题3分,满分15分,把答案填在题中横线上.)
(1)【答案】
【解析】这是
型未定式求极限.
方法一： 
,
令
,则当
时,
,
则 
,
即 
.
由题设有
,得
.
方法二：
,
由题设有,得.
(2)【答案】
【解析】方法一：所求平面过原点
与
,其法向量
；平面垂直于已知平面,它们的法向量也互相垂直：
；
由此, 
.
取
,则所求的平面方程为.
方法二：所求平面即为过原点,与两个不共线的向量(一个是从原点到点的向量
,另一是平面的法向量
)平行的平面,
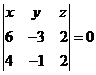即 
,即 .
(3)【答案】
【解析】微分方程所对应的齐次微分方程的特征方程为
,解之得
.故对应齐次微分方程的解为
.
由于非齐次项
不是特征根,设所给非齐次方程的特解为
,代入
得
(也不难直接看出
),故所求通解为
.
【相关知识点】① 二阶线性非齐次方程解的结构：设
是二阶线性非齐次方程
的一个特解.
是与之对应的齐次方程
的通解,则
是非齐次方程的通解.
② 二阶常系数线性齐次方程通解的求解方法：对于求解二阶常系数线性齐次方程的通解,可用特征方程法求解：即中的
、
均是常数,方程变为
.其特征方程写为
,在复数域内解出两个特征根
；
分三种情况：
(1) 两个不相等的实数根,则通解为
(2) 两个相等的实数根
,则通解为
(3) 一对共轭复根
,则通解为
其中
为常数.
③ 对于求解二阶线性非齐次方程的一个特解,可用待定系数法,有结论如下：
如果
则二阶常系数线性非齐次方程具有形如
的特解,其中
是与
相同次数的多项式,而按不是特征方程的根、是特征方程的单根或是特征方程的重根依次取0、1或2.
如果
,则二阶常系数非齐次线性微分方程
的特解可设为
,
其中
与
是
次多项式,
,而按
(或
)不是特征方程的根、或是特征方程的单根依次取为
或
.
(4)【答案】
【分析】先求方向
的方向余弦和
,然后按方向导数的计算公式
求出方向导数.
【解析】因为与
同向,为求的方向余弦,将
单位化，即得 
.
将函数分别对
求偏导数得
,
,
,
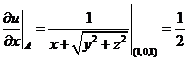所以 
&nbs
