时间:2016-03-05 18:00:44
1987年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)
(1)当![]() =_____________时,函数
=_____________时,函数![]() 取得极小值.
取得极小值.
(2)由曲线![]() 与两直线
与两直线![]() 及
及![]() 所围成的平面图形的面积是_____________.
所围成的平面图形的面积是_____________.
![]()
![]()
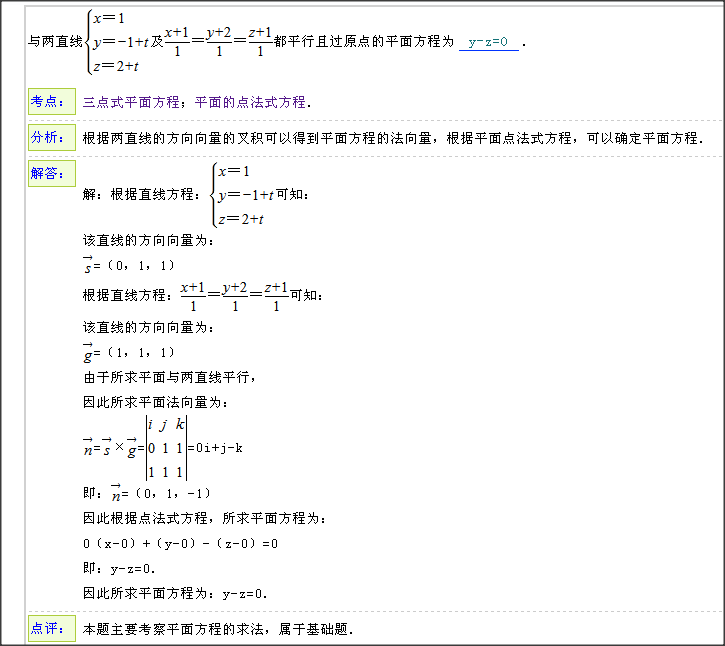
(3)与两直线 ![]()
![]()
及![]() 都平行且过原点的平面方程为_____________.
都平行且过原点的平面方程为_____________.
(4)设![]() 为取正向的圆周
为取正向的圆周![]() 则曲线积分
则曲线积分![]() = _____________.
= _____________.
(5)已知三维向量空间的基底为![]() 则向量
则向量![]() 在此基底下的坐标是_____________.
在此基底下的坐标是_____________.
二、(本题满分8分)
求正的常数![]() 与
与![]() 使等式
使等式![]() 成立.
成立.
三、(本题满分7分)
(1)设![]() 、
、![]() 为连续可微函数
为连续可微函数![]() 求
求![]()
(2)设矩阵![]() 和
和![]() 满足关系式
满足关系式![]() 其中
其中 求矩阵
求矩阵![]()
四、(本题满分8分)
求微分方程![]() 的通解,其中常数
的通解,其中常数![]()
五、选择题(本题共4小题,每小题3分,满分12分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(1)设![]() 则在
则在![]() 处
处
(A)![]() 的导数存在,且
的导数存在,且![]() (B)
(B)![]() 取得极大值
取得极大值
(C)![]() 取得极小值 (D)
取得极小值 (D)![]() 的导数不存在
的导数不存在
(2)设![]() 为已知连续函数
为已知连续函数![]() 其中
其中![]() 则
则![]() 的值
的值
(A)依赖于![]() 和
和![]() (B)依赖于
(B)依赖于![]() 、
、![]() 和
和![]()
(C)依赖于![]() 、
、![]() ,不依赖于
,不依赖于![]() (D)依赖于
(D)依赖于![]() ,不依赖于
,不依赖于![]()
(3)设常数![]() 则级数
则级数![]()
(A)发散 (B)绝对收敛
(C)条件收敛 (D)散敛性与![]() 的取值有关
的取值有关
(4)设![]() 为
为![]() 阶方阵,且
阶方阵,且![]() 的行列式
的行列式![]() 而
而![]() 是
是![]() 的伴随矩阵,则
的伴随矩阵,则![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
六、(本题满分10分)
求幂级数![]() 的收敛域,并求其和函数.
的收敛域,并求其和函数.
七、(本题满分10分)
求曲面积分
![]()
其中![]() 是由曲线
是由曲线 绕
绕![]() 轴旋转一周而成的曲面,其法向量与
轴旋转一周而成的曲面,其法向量与![]() 轴正向的夹角恒大于
轴正向的夹角恒大于![]()
八、(本题满分10分)
设函数![]() 在闭区间
在闭区间![]() 上可微,对于
上可微,对于![]() 上的每一个
上的每一个![]() 函数
函数![]() 的值都在开区间
的值都在开区间![]() 内,且
内,且![]() 1,证明在
1,证明在![]() 内有且仅有一个
内有且仅有一个![]() 使得
使得![]()
九、(本题满分8分)
问![]() 为何值时,现线性方程组
为何值时,现线性方程组
![]()
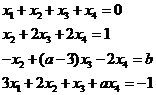
有唯一解,无解,有无穷多解?并求出有无穷多解时的通解.
十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)
(1)设在一次实验中,事件![]() 发生的概率为
发生的概率为![]() 现进行
现进行![]() 次独立试验,则
次独立试验,则![]() 至少发生一次的概率为____________;而事件
至少发生一次的概率为____________;而事件![]() 至多发生一次的概率为____________.
至多发生一次的概率为____________.
(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________.
(3)已知连续随机变量![]() 的概率密度函数为
的概率密度函数为![]() 则
则![]() 的数学期望为____________,
的数学期望为____________,![]() 的方差为____________.
的方差为____________.
十一、(本题满分6分)
设随机变量![]() 相互独立,其概率密度函数分别为
相互独立,其概率密度函数分别为
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() , 求
, 求![]() 的概率密度函数.
的概率密度函数.
1987年全国硕士研究生入学统一考试数学一试卷 一(1) 一(2) 一(3) 一(4) 一(5) 二. 三(1). 三(2) 四 五(1) 五(2) 五(3) 五(4) 六. 七. 八. 九. 十(1) 十(2) 十(3) 十一. 





 ……
……













