时间:2016-03-05 16:09:22
![]()
22.(本题满分11分)
设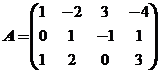 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
(1) 求方程组![]() 的一个基础解系;
的一个基础解系;
(2) 求满足![]() 的所有矩阵.
的所有矩阵.
【详解】(1)对系数矩阵A进行初等行变换如下:
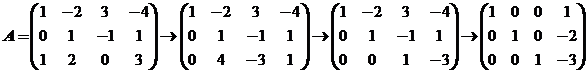 ,
,
得到方程组![]() 同解方程组
同解方程组
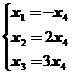
得到![]() 的一个基础解系
的一个基础解系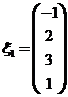 .
.
(2)显然B矩阵是一个![]() 矩阵,设
矩阵,设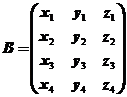
对矩阵![]() 进行进行初等行变换如下:
进行进行初等行变换如下:
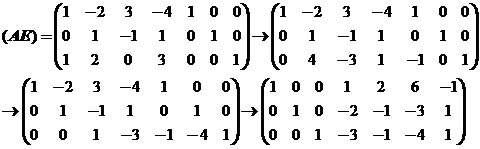
由方程组可得矩阵B对应的三列分别为
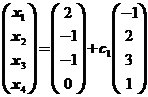 ,
,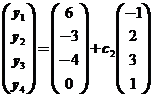 ,
,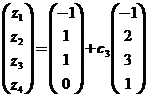 ,
,
即满足![]() 的所有矩阵为
的所有矩阵为
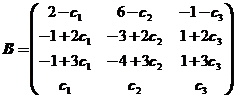
其中![]() 为任意常数.
为任意常数.
23.(本题满分11分)
证明![]() 阶矩阵
阶矩阵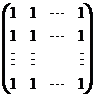 与
与 相似.
相似.
【详解】证明:设![]()
 ,
,![]()
 .
.
分别求两个矩阵的特征值和特征向量如下:
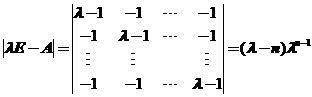 ,
,
所以A的![]() 个特征值为
个特征值为![]() ;
;
而且A是实对称矩阵,所以一定可以对角化.且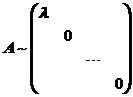 ;
;
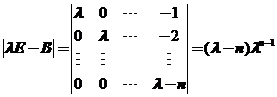
所以B的![]() 个特征值也为
个特征值也为![]() ;
;
对于![]() 重特征值
重特征值![]() ,由于矩阵
,由于矩阵![]() 的秩显然为1,所以矩阵B对应
的秩显然为1,所以矩阵B对应![]() 重特征值
重特征值![]() 的特征向量应该有
的特征向量应该有![]() 个线性无关,进一步矩阵B存在
个线性无关,进一步矩阵B存在![]() 个线性无关的特征向量,即矩阵B一定可以对角化,且
个线性无关的特征向量,即矩阵B一定可以对角化,且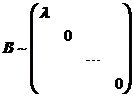
从而可知![]() 阶矩阵
阶矩阵 与
与 相似.
相似.