时间:2017-02-06 08:28:50
1、单选题 (2009-北京社会)甲、乙、丙三个滑冰运动员在一起练习滑冰,已知甲滑一圈的时间,乙、丙分别可以滑一又四分之一圈和一又六分之一圈,若甲、乙、丙同时从起点出发,则甲滑多少圈后三人再次在起点相遇?_____
A: 8
B: 10
C: 12
D: 14
参考答案: C
本题解释:参考答案:C
题目详解:根据题意,“三人再次在起点相遇”,则三人滑的圈数必须都为整数;相同时间内,甲、乙、丙滑的圈数之比为:
2、单选题 对一批编号为1—100,全部开关朝上(开)的灯进行一下操作:凡是1的倍数反方向拨一次开关;2的倍数反方向又拨一次开关;3的倍数反方向又拨一次开关;一直到100的倍数。则最后状态为关的灯有几个?_____
A: 10
B: 15
C: 20
D: 大于20
参考答案: A
本题解释:参考答案:A
题目详解:最后处于关闭状态的灯,其开关被拨动的次数为奇数,因此该题转化为:求1—100中有多少个数其约数个数为奇数。根据约数的定义:如果b为a的约数,则有a=bc(c为整数),故除了b=c,即a为完全平方数这种情况之外,a的约数个数一定都是偶数。由于
3、单选题 甲、乙两人各写一个三位数,发现这两个三位数有两个数字是相同的,并且它们的最大公约数是75,那么这两个三位数的和的最大值是多少?_____
A: 1725
B: 1690
C: 1545
D: 1340
参考答案: A
本题解释:参考答案:A
题目详解:由题意可知:75的倍数的最大三位数是:13×75=975;有两个数字相同的另一个75的倍数最大的是:10×75=750;所以,这两个三位数的和的最大值是:975+750=1725。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数
4、单选题 有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果平均分给一些小朋友,已知苹果分到最后余2个,桔子分到最后还余7个,求最多有多少个小朋友参加分水果?_____
A: 14
B: 17
C: 28
D: 34
参考答案: D
本题解释:参考答案
题目详解:根据题意,由于苹果分到最后余2,桔子分到最后余7,那么: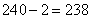
5、单选题 在1到200的全部自然数中,既不是5的倍数,也不是8的倍数的数有多少个?_____
A: 25
B: 40
C: 60
D: 140
参考答案: D
本题解释:参考答案
题目详解:由题意得,5和8的最小公倍数是40。从1到200中,5的倍数有:200÷5=40个,8的倍数有:200÷8=25个,5和8的公倍数有:200÷40=5个,至少是5或者8的倍数的有:40+25-5=60个。所以,既不是5的倍数,也不是8的倍数的数有:200-60=140个。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数