时间:2017-01-17 00:37:45
1、单选题 某通讯公司对3542个上网客户的上网方式进行调查，其中1258个客户使用手机上网，1852个客户使用有线网络上网，932个客户使用无线网络上网。如果使用不只一种上网方式的有352个客户，那么三种上网方式都使用的客户有多少个?_____
A: 148
B: 248
C: 350
D: 500
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，只使用一种方式上网的有(3542-352)个，根据题意可得：1258+1852+932=(3542-352)+2×(352-y)+3×y，解得y=148，因此三种上网方式都使用的客户有148个，故正确答案为A。解析2：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，前者重复计算了2次，后者重复计算了1次，根据题意可得：1258+1852+932-2y-(352-y)=3542，解得y=148，此三种上网方式都使用的客户有148个，故正确答案为A。备注：三集合容斥原理中，将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z。标签三集合容斥原理公式整体考虑公式应用
2、单选题 地铁工程在某1000米路段地下施工，两头并进，一侧地铁盾沟机施工，每天掘进3米，工作5天，休息一天进行检修；另一侧工人轮岗不休，每天掘进1米，多少天此段打通_____
A: 282
B: 285
C: 286
D: 288
参考答案: C
本题解释:【答案】C。解析：一侧工程队6天挖3×5=15米，另一侧工程队6天挖6米，以6天为一个周期，两个工程队一个周期一共挖了21米，1000米的路段一共需要1000÷21=47…13。一共需要47个整周期，还余13米，两侧工程队一起挖还需要4天，所以一共需要47×6+4=286天。
3、单选题 自然数P满足下列条件：P除以10的余数为9，P除以9的余数为8，P除以8的余数为7。如果：100＜P＜1000，则这样的P有几个？_____
A: 不存在
B: 1个
C: 2个
D: 3个
参考答案: C
本题解释:正确答案是C解析由"
除以10的余数为9，P除以9的余数为8，P除以8的余数为7"，满足差同减差，对应口诀可知其符合表达式为360n－1，由于100＜P＜1000，则100＜360n－1＜1000，所以n能取1、2，则满足条件的P有两个，即359和719，故正确答案为C。注释：同余问题需要掌握如下口诀：余同取余，和同加和，差同加差，最小公倍数做周期。口诀解释：余同取余，例如"一个数除以7余1，除以6余1，除以5余1"，可见所得余数恒为1，则取1，被除数的表达式为210n＋1；和同加和，例如"一个数除以7余1，除以6余2，除以5余3"，可见除数与余的和相同，取此和8，被除数的表达式为210n＋8；差同减差，例如"一个数除以7余3，除以6余2，除以5余1"，可见除数与余的差相同，取此差4，被除数的表达式为210n－4。特别注意前面的210是5、6、7的最小公倍数。余数与同余问题标签同余问题
4、单选题 一个工人加工一批产品，他每加工出一件正品，得报酬0.75元，每加工出一件次品，罚款1.50元。这天他加工的正品是次品的7倍，得款11.25元。那么他这天加工出多少件次品?_____
A: 1
B: 3
C: 7
D: 13
参考答案: B
本题解释:B【解析】 工人加工7件正品得款0.75×7=5.25（元），加工出一件次品罚款1.50元，所以每加工8件产品得款5.25-1.50=3.75（元）。所以他这天加工出的次品是11.25÷3.75=3（件）。
5、单选题 有3根钢丝，第一根的长度是第二根的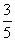 
A: 10
B: 11
C: 12
D: 15
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，可知：第一根:第二根=3:5，第一根:第三根=3:4，所以，第二根:第三根=5:4;所以第二根长384÷(5-4)×5=1920毫米，第一根长1920÷5×3=1152毫米，第三根长1920÷5×4=1536毫米;截成的小段长为三根钢丝长度的最大公约数，(1152，1920，1536)=384毫米，所以这三根钢丝截成了(1152+1920+1536)÷384=12根。因此，选C。考查点:数量关系>数学运算>和差倍比问题>比例问题