时间:2017-01-14 01:04:11
1、单选题 网管员小刘负责甲、乙、丙三个机房的巡检工作,甲、乙和丙机房分别需要每隔2天、4天和7天巡检一次。3月1日,小刘巡检了3个机房,问他在整个3月有几天不用做机房的巡检工作:_____
A: 12
B: 13
C: 14
D: 15
参考答案: C
本题解释:正确答案是C,解析方法一:根据三集合容斥原理的标准公式:需要工作的天数为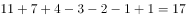
2、单选题 甲乙丙丁四个数的和为43,甲数的2倍加8,乙数的3倍,丙数的4倍,丁数的5倍减去4,都相等。这四个数各是多少?_____
A: 141289
B: 161296
C: 1110814
D: 141298
参考答案: D
本题解释:正确答案是D考点计算问题解析解法1:设甲数为a,乙数为b,丙数为c,丁数为d,由题意有:
3、单选题 有绿、白两种颜色且尺寸相同的正方形瓷砖共400块,将这些瓷砖铺在一块正方形的地面上:最外面的一周用绿色瓷砖铺,从外往里数的第二周用白色瓷砖铺,第三周用绿色瓷砖,第四周用白色瓷砖……这样依次交替铺下去,恰好将所有瓷砖用完。这块正方形地面上的绿色瓷砖共有_____块。
A: 180
B: 196
C: 210
D: 220
参考答案: D
本题解释:正确答案是D考点数列问题解析由瓷砖总数为400块,可知该正方形边长为20块瓷砖,每往里一层,边长减少2块瓷砖,由此可知每往里一层绿色瓷砖,边长减少4块瓷砖。因此绿色瓷砖共5层,最外层一圈为76块砖,最里一层一圈为12块砖,总数为(76+12)÷2×5=220块。故正确答案为D。注:等差数列求和公式,和=(首项+末项)×项数÷2标签公式应用
4、单选题 如下图所示,AB两点是圆形体育场直径的两端,两人从AB点同时出发,沿环形跑道相向匀速而行,他们在距A点弧形距离80米处的C点第一次相遇,接着又在距B点弧形距离60米处的D点第二次相遇,问这个圆形体育场的周长是多少米?_____ A: 240
A: 240
B: 300
C: 360
D: 420
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1:根据题意可知两人第一个运动过程的路程和为半个圆周,第二个运动过程的路程和为整个圆周,因此每个人在两个过程中的路程比为1:2,设劣弧BC长为x,根据题意可得,80:(x+60)=1:2,解得x=100,因此圆周长为:2×(80+100)=360,故正确答案为C。解析2:此题为两次相遇问题,运用公式可得圆周长的一半为:80×3-60=180米,因此周长为360米,故正确答案为C。备注:两次相遇问题,两边型的两端点之间的距离公式:S=3A-B,其中S表示两端点之间的距离,A、B表示先后两次相遇点分别关于两个端点的距离。
5、单选题 A、B、C三辆卡车一起运输1次,正好能运完一集装箱的某种货物。现三辆卡车一起执行该种货物共40集装箱的运输任务,A运7次、B运5次、C运4次,正好运完5集装箱的量。此时C车休息,而A、B车各运了21次,又完成了12集装箱的量。问如果此后换为A、C两车同时运输,至少还需要各运多少次才能运完剩余的该种货物?_____
A: 30
B: 32
C: 34
D: 36
参考答案: D
本题解释:正确答案是D,全站数据:本题共被作答1次,正确率为0.00%,易错项为A解析根据题意列方程A+B+C=1••••••①,7A+5B+4C=5••••••②,21A+21B=12••••••③,由①和②可得,2A=C,所以将③化为7A+7C+7B+14B=12所以得到B=5/14,再代入①得到,A+C=9/14所以23÷(9/14)÷asymp;36。故正确答案为D。速解本体是典型的工程问题,需要靠方程组求解,在求解方程组的过程中,消元的方式比较多,不必局限于一种解法。考点工程问题