时间:2017-01-03 13:32:39
1、单选题 园林工人要在周长300米的圆形花坛边等距离栽树。他们先沿着花坛的边每隔3米挖一个坑,当挖完30个坑时,突然接到通知:改为每隔5米栽一棵树。这样,他们还要挖多少个坑才能完成任务?_____
A: 43个
B: 53个
C: 54个
D: 60个
参考答案: C
本题解释:正确答案是C考点计数模型问题解析300米的圆形花坛边等距离栽树,每隔5米栽一棵,根据单边环形植树公式得要挖300/5=60个坑,先前按照每隔3米栽一棵树,挖了30个坑,从第1个坑到第30个坑的距离可用单边线性植树公式求得为(30-1)×3=87米,因此需找出已经挖的这些坑中能被利用的,若能被利用,则它距离第一个坑的距离就能被15(3和5的最小公倍数)整除,0至87之间能被15整除的数有6个(0、15、30、45、60、75),所以还需挖60-6=54个坑,故正确答案为C。公式:单边环形植树:棵树=总长÷间隔。单边线性植树:总长=(棵树-1)×间隔。标签最小公倍数公式应用
2、单选题 (2006广东上,第14题)有一个灌溉用的中转水池,-直开着进水管往里灌水,-段时间后,用2台抽水机排水,则用40分钟能排完;如果用4台同样的抽水机排水,则用l6分钟排完。问如果计划用10分钟将水排完,需要多少台抽水机?_____
A: 5台
B: 6台
C: 7台
D: 8台
参考答案: B
本题解释:参考答案:B
题目详解:依题意:设原有水量为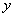
3、单选题 把一个边长为4厘米的正方形铁丝框拉成两个同样大小的圆形铁丝框,则每个圆铁丝框的面积为_____。 A: A
A: A
B: B
C: C
D: D
参考答案: D
本题解释:D【解析】设铁丝拉成的圆的半径为r,则4×4=2×2πr,r=
4、单选题 去超市购买商品,如果购买9件甲商品,5件乙商品和1件丙商品一共需要72元。如果购买13件甲商品,7件乙商品和1件丙商品一共需要86元。若甲、乙、丙三种商品各买2件,共需要多少钱?_____
A: 88
B: 66
C: 58
D: 44
参考答案: A
本题解释:正确答案是A考点不定方程问题解析解析1:设甲、乙、丙的价格分别为A、B、C元,根据题意,9A+5B+C=72,13A+7B+C=86,这是一个不定方程,可设A=0,容易解出B=7,C=37,则2(A+B+C)=88(元),故正确答案为A。解析2:设甲、乙、丙的价格分别为A、B、C元,根据题意,9A+5B+C=72①,13A+7B+C=86②,两个方程相减得2A+B=7③,①+②-11③=B+2C=81,故(2A+B)+(B+2C)=7+81=2A+2B+2C=88(元),故正确答案为A。
5、单选题 某市居民生活用电每月标准用电量的基本价格为每度0.60元,若每月用电量超过标准用电量,超出部分按照基本价格的80%收费。某户九月份的用电量为100度,共交电费57.60元,则该市每月标准用电量为_____。
A: 60度
B: 70度
C: 80度
D: 90度
参考答案: C
本题解释:正确答案是C考点鸡兔同笼问题解析解析1:若按基本价格收费,用电量100度应交电费60元,现交57.6元,少交2.4元,则按照基本价格80%收费的用电量为2.4÷(0.6×20%)=20度,即标准用电量为100-20=80度。解析2:设该市标准用电量为A度,根据题意有:0.6A+0.6×0.8(100-A)=57.6,解得A=80,故正确答案为C。