时间:2016-06-16 22:22:11
1、袋子里红球与白球的数量之比为19∶13,放入若干个红球后,红球与白球的数量之比变为5∶3,再放入若干个白球后,红球与白球的数量之比为13∶11,已知放入的红球比白球少80个。那么原来袋子里共有多少个球?_____
A: 650 B: 720 C: 840 D: 960
参考答案: D 本题解释:
2、有100人参加运动会的三个比赛项目,每人至少参加一项,其中未参加跳远的有50人,未参加跳高的有60人,未参加赛跑的有70人。问至少有多少人参加了不止一个项目?_____
A: 7 B: 10 C: 15 D: 20
参考答案: B 本题解释:【解析】B.最值问题。由题意,参加跳远的人数为50人,参加跳高的为40人,参加赛跑的为30人;即参加项目的人次为120人次;故欲使参加不止一项的人数最少,则需要使只参加一项的人数最多为x,参加3项的人数为y;故x+3y=120,x+y=100,解得y=10
3、某汽车厂离生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为_____。
A: 5:4:3B: 4:3:2C: 4:2:1D: 3:2:1
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设甲的产量为x,乙的产量为y,丙的产量为z。则可得如下:3y+6z=4x,x+2y=7z,两式相加可得3x+z=5y,直接带入选项,只有D符合,故正确答案为D。秒杀技得到3y+6z=4x后,观察该式,可知x应为3的倍数,只有D符合。标签直接代入
4、某服装厂要生产一批某种型号的学生服,已知每3米长的某种面料可做上衣2件。或做裤子3条,计划用300米长的这种布料生产学生服,应用多少米布料产生上衣,才能恰好配套?_____
A: 120B: 150C: 180D: 210
参考答案: C 本题解释:答案:C【解析】3米长可做上衣2件,或裤子3条,则300米布料可做上衣200件,或裤子300条,即如需成套,则上衣和裤子的数量必须同样多,那么上衣所用布料当为3/5,即180米,裤子为120米,共可做120套服装。所以答案为选项C。
5、某次抽奖活动在三个箱子中均放有红、黄、一绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少?_____
A: 在 0~25%之间B: 在25~50%之间C: 在50~75%之间D: 在75~100%之间
参考答案: C 本题解释:C。
6、一家公司2006年的月累计利润y(单位:万元)与月份x的变化关系如下表所示: 则该公司2006年的月平均利润是_____万元。
则该公司2006年的月平均利润是_____万元。
A: 15B: 16C: 21D: 30
参考答案: C 本题解释:正确答案是C解析把x=1和x=2代入可得1+b+c=21,4+2b+c=32,联立解得b=8,c=12。当x=12时,y=12×12+8×12+12=252万元,月平均利润为252÷12=21万元,故正确答案为C。考点经济利润问题
7、足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,如果某国家足球队共打了28场比赛,其中负6场,共得40分,那么这个队胜了多少场?_____
A: 8B: 10C: 12D: 9
参考答案: D 本题解释:正确答案是D考点鸡兔同笼问题解析解析1:这是鸡兔同笼问题的推广得得失问题,胜的场数和平的场数共有28-6=22(场),根据得失问题公式,则胜的场数为(40-22)÷(3-1)=9(场),故选D选项。注:比赛得失问题公式,﹙总的得分-平场数×平场得分)÷(胜场得分-平场得分)=胜的场数,(只有胜和平场时);(总的得分-平的场数×平场得分+输的场数×输场扣分)÷(胜场得分-平场得分+输场扣分)=胜的场数,(有胜、平、输场时)。解析2:胜的场数和平的场数共有28-6=22(场),设胜的胜数为a,3×a+1×(22-a)=40,a=9(场),故正确答案为D。标签公式应用
8、已知两个数a、b的积是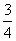 ,和是2,且a>b,则
,和是2,且a>b,则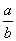 的值是:_____
的值是:_____
A: 3B: 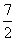 C: 4D:
C: 4D: 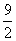
参考答案: A 本题解释:参考答案:A题目详解:解法一:由题意可知: ,
, ,解得:
,解得: 则:
则: 由于
由于 ,所以:
,所以: ,
, ,所以
,所以 解法二:ab的积乘以
解法二:ab的积乘以 得到a的平方,看下答案,什么数乘以
得到a的平方,看下答案,什么数乘以 得到的结果是可以开平方的。判断得到是A
得到的结果是可以开平方的。判断得到是A 是a=
是a= 的平方,省略了计算,也可验证
的平方,省略了计算,也可验证 ,
, ,符合题目要求。(该解析由用户“小爱行测加油”于2011-03-0613:24:15贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
,符合题目要求。(该解析由用户“小爱行测加油”于2011-03-0613:24:15贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
9、一段路程分为上坡、平路、下坡,三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米,路程全长是50千米,小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析:上坡、平路、下坡的速度之比是:14∶25∶36=5∶8∶10平路速度为:3×8/5=24/5(千米/小时)下坡速度为:3×10/5=6(千米/小时)上坡路程为:50×1/(1+2+3)=50/6=25/3(千米)平路路程为:50×2/(1+2+3)=50/3(千米)下坡路程为:50×3/(1+2+3)=25(千米)小龙走完全程用的时间为:25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。
10、加油站有150吨汽油和102吨柴油,每天销售12吨汽油和7吨柴油。问多少天后,剩下的柴油是剩下的汽油的3倍?_____
A: 9B: 10C: 11D: 12
参考答案: D 本题解释:【答案】D。解析:假设x天,汽油还剩150-12x,柴油还剩102-7x,102-7x=3(150-12x),解得x=12,答案为D。
11、商场的自动扶梯以匀速由下往上行驶,两个孩子在行驶的扶梯上上下走动,女孩由下往上走,男孩由上往下走,结果女孩走了40级到达楼上,男孩走了80级到达楼下。如果男孩单位时间内走的扶梯级数是女孩的2倍。则当该扶梯静止时,可看到的扶梯梯级有_____。
A: 40级B: 50级C: 60级D: 70级
参考答案: C 本题解释:正确答案是C考点行程问题解析解析1:设女孩的速度为x,男孩为2x,扶梯的速度为y,根据题意可知男孩和女孩所用的时间相同,有x+y=2x-y,得x:y=2,即女孩的速度为扶梯的2倍,因此当女孩走了40级时扶梯走了20级,扶梯静止时有60级。因此正确答案为C。解析2:因为男孩单位时间内走的扶梯级数是女孩的2倍,所以男孩走80级的时间和女孩走40级的时间相等,由此可知他们两个乘电梯的时间相同,则电梯运行距离也相等,也即有如下两式:对于男孩:电梯长度=80-电梯运行距离;对于女孩:电梯长度=40+电梯运行距离。由此可知电梯长度为60,故正确答案为C。
12、有关部门要连续审核30个科研课题方案,如果要求每天安排审核的课题个数互不相等且不为零,则审核完这些课题最多需要_____。
A: 7天B: 8天C: 9天D: 10天
参考答案: A 本题解释:参考答案:A题目详解:每天审核的课题应尽可能少,才能增加审核天数。假设第1天审核1个,则第2天最少审核2个,……依此类推,则审核完这些课题天数最多的方案应为每天审核1,2,3,4,5,6,9或1,2,3,4,5,7,8。显然所需天数都为7天。所以,选A。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
13、甲乙丙的速度之比为3:4:5,经过相同的一段路,三人所用时间之比:_____
A: 3:4:5 B: 5:4:3 C: 20:15:12 D: 12:8:5
参考答案: C 本题解释:C【解析】根据公式“时间=路程÷速度”可知,经过相同的路程,甲、乙、丙的时间比为1/3:1/4:1/5=20:15:12。
14、某工厂11月份工作忙,星期六、日不休息,而且从第一天开始,每天下班后都从总厂陆续派相同人数的工人到分厂工作,直到月底下班后,总厂还剩工人238人。如果月底统计总厂工人的工作量是8070个工作日(1人工作1天为1个工作日),且无1个缺勤,那么,这个月由总厂派到分厂工作的工人共多少人?_____
A: 46人B: 30人C: 60人D: 62人
参考答案: C 本题解释:11月份有30天。设每天下班后派往分厂的人数为2,则根据题意可知,最后一天总厂的工作量为238+z,可列方程238+x+238+2x+…+238+30x=8070,解得x=2,即每天派2人到分厂工作,11月份30天共派了60人到分厂。故答案为C。
15、正方体 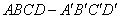 中,侧面对角线
中,侧面对角线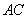 与
与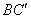 所成的角等于_____。
所成的角等于_____。 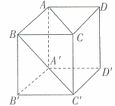
A: 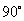 B:
B: 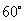 C:
C: 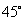 D:
D: 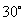
参考答案: B 本题解释:参考答案:B题目详解:根据题意,连接 与
与 。∵
。∵ ∴
∴ 为等边三角形,又∵
为等边三角形,又∵ 与
与 平行,∴侧面对角线
平行,∴侧面对角线 与
与 所成的角等于
所成的角等于 。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
。因此,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
16、某船第一次顺流航行21千米又逆流航行4千米,第二天在同 河道中顺流航行12千米,逆流航行7千米,结果两次所用的时间相等。假设船本身速度及水流速度保持不变,则顺水船速与逆水船速之比是_____。
A: 2. 5:1 B: 3:1 C: 3. 5:1 D: 4:1
参考答案: B 本题解释:【解析】B。设船本身速度为 X 千米 / 小时,水流速度为 Y 千米 / 小时,则顺水船速为 (X+Y) 千米 / 小时,逆水船速为 (X-Y) 千米 / 小时。依据题意可得: 21X+Y+4X-Y = 12X+Y+7X-Y ,由此可得 X+YX-Y = 3 ,即顺水船速是逆水船速的 3 倍。
17、李明从图书馆借来一批图书,他先给了甲5本和剩下的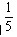 ,然后给了乙4本和剩下
,然后给了乙4本和剩下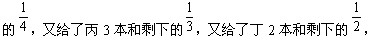 ,最后自己还剩2本。李明共借了多少本书?_____
,最后自己还剩2本。李明共借了多少本书?_____
A: 30B: 40C: 50D: 60
参考答案: A 本题解释: 【解析】A。解法一、设李明共借书x本,则 ,解得x=30;解法二、思维较快的直接倒推用反计算,
,解得x=30;解法二、思维较快的直接倒推用反计算, 。
。
18、一杯糖水,第一次加入一定量的水后,糖水的含糖百分比变为15%;第二次又加入同样多的水,糖水的含糖百分变比为12%;第三次再加入同样多的水,糖水的含糖百分比将变为多少?_____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:【答案】C。解析: 故正确答案为C。
故正确答案为C。
19、某社团共有46人,其中36人爱好戏剧,30人爱好体育,38人爱好写作,40人爱好收藏,问这个社团至少有_____人以上四项活动都喜欢。
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:【答案解析】根据题意可知,不爱好戏剧的有46-36=10人,不爱好体育的有46-30=16人,不爱好写作的有46-38=8人,不爱好收藏的有46-40=6人。要使四项活动都喜欢的人最少,则应使不爱好这四项活动的人最多,即使不爱好这四项活动的人均不重复,所以至少有46-(10+16+8+6)=6人四项活动都喜欢。所以正确答案为B项。
20、一项工程如果交给甲乙两队共同施工,8天能完成;如果交给甲丙两队共同施工,10天能完成;如果交给甲丁两队共同施工,15天能完成;如果交给乙丙丁三队共同施工,6天就可以完成。如果甲队独立施工,需要多少天完成?_____
A: 16 B: 20C: 24D: 28
参考答案: C 本题解释:【解析】C。本题为工程问题,设工作总量为120,则甲乙工作效率和为15、甲丙工作效率和为12、甲丁工作效率和为8、乙丙丁效率和为20,可得甲的效率为(15+12+8-20)÷3=5,则甲单独完成需要120÷5=24天。所以选择C选项。
21、将两位数的个位数与十位数互换后所得的数是原来的十分之一,这样的两位数有多少个?_____
A: 6B: 9C: 12D: 15
参考答案: B 本题解释:B【解析】设原数字的个位数字为x,十位数字为y,则得:(10y+x)X1/10=10x+y化简得x=0个位数字是0的两位数有10,20,30,40,50,60,70,80,90,共9个,故正确答案为B。
22、甲、乙两人进行乒乓球比赛,比赛采取三局两胜制,无论哪一方先胜两局则比赛结束。甲每局获胜的概率为2/3,乙每局获胜的概率为1/3。问甲最后取胜的概率是多少?_____
A: AB: BC: CD: D
参考答案: A
23、足球比赛的记分规则为:胜一场得3分;平一场得1分;负一场得0分。一个队打了14场,负5场,共得19分,那么这个队胜了几场?_____
A: 3 B: 4 C: 5 D: 6
参考答案: C 本题解释: 【解析】C。设这个队胜了X场,可得方程3X+9-X=19,得X=5,所以此队胜了5场。
24、某船第一次顺流航行21千米又逆流航行4千米,第二次在同一河道中顺流航行12千米,逆流航行7千米,结果两次所用的时间相等。则顺水船速与逆水船速之比是_____。(设船本身的速度及水流的速度都是不变的)
A: 4∶1B: 3∶1C: 2∶1D: 9∶1
参考答案: B 本题解释:B 【解析】船第一次顺流航行21千米,第二次顺流航行12千米,21-12=9,也就是第一次顺流多用了航行9千米所用的时间,第二次逆流比第一次多用时间于3千米的航行上,总的两次时间相等。就是顺流9千米用的时间等于逆流3千米所用的时间。顺流船速:逆流船速=(21-12)∶(7-4)=3∶1,即顺水船速是逆水船速的3倍。
25、甲、乙两港相距720千米,轮船往返两港需要35小时,逆流航行比顺流航行多花5个小时;帆船在静水中每小时行驶24千米,问帆船往返两港需要多少小时?_____
A: 58B: 60C: 64D: 66
参考答案: C 本题解释:C。分析可知轮船逆流航行了20小时,顺流航行了15小时。可得水流速度是(720÷15—720÷20)÷2=6千米/小时,所以帆船顺水速度是24+6=30千米/小时,逆水速度是24—6=18千米/小时,往返需要720÷30+720÷18=64小时。
26、某商场举行周年让利活动,单件商品满300减180元,满200减100元,满100减40元;若不参加活动则打5.5折。小王买了价值360元,220元,150元的商品各一件,最少需要多少元钱?_____
A: 360B: 382.5C: 401.5D: 410
参考答案: B 本题解释:【答案】B。解析:如下表: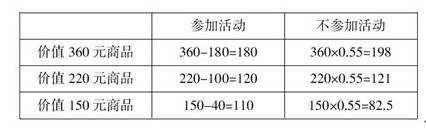 因此最少需要180+120+82.5=382.5元。
因此最少需要180+120+82.5=382.5元。
27、某单位职工24人中,有女性11人,已婚的有16人。在婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释:答案:B【解析】男性人数为:24-11=13,已婚男性为l6-6=10(人),因此,未婚男性为13-10=3(人),故选B。
28、一名事业单位职工1978年参加工作时月工资总额是49.5元,2012年其年工资是1978年的112倍且每月还多11元,改革开放以来这名职工月工资增加了多少元?_____
A: 5050B: 5505.5C: 5545D: 5555.5
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析改革开放以来该职工月工资增长量是1978年工资的111倍还多11元,也即:49.5×111+11=49.5×111+11=5505.5元,故正确答案为B。
29、某公司甲、乙两个营业部共有50人,其中32人为男性。已知甲营业部的男女比例为5:3,乙营业部的男女比例为2:1,问甲营业部有多少名女职员?_____
A: 18B: 16C: 12D: 9
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设甲营业部有3X名女职员,乙营业部有Y名女职员,则有5X+2Y=32;32+3X+Y=50,解得X=4,Y=6,故甲营业部有3×4=12名女职员,故正确答案为C。秒杀技有题意可知,两个营业部共有50-32=18名女职员,排除A。根据“乙营业部的男女比例为2:1”可知,乙营业部的男职员为偶数,由于男职员的总人数为偶数,则甲营业部的男职员人数同样为偶数。根据“已知甲营业部的男女比例为5:3”,甲营业部的女职员人数能同时被2和3整除,排除B、D,故正确答案为C。
30、从一楼走到五楼,爬完一层休息30秒,一共要210秒,那么从一楼走到7楼,需要多少秒?_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:【答案】C。解析:从一楼走到五楼,休息了3次,那么每爬上一层需要的时间为(210-30×3)÷4=30秒,故从一楼走到七楼需要30×(7-2)+30×(7-1)=330秒。故正确答案为C。
31、一根木杆,第一次截去了全长的1/2,第二次截去所剩木杆的1/3,第三次截去所剩木杆的1/4,第四次截去所剩木杆的1/5,这时量得所剩木杆长为6厘米。问:木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:C解析:6÷(1-1/5)÷(1-1/4)÷(1-1/3)÷(1-1/2)=6÷(4/5×3/4×2/3×1/2)=6÷1/5=30(厘米)故本题选C。
32、某储户于1999年1月1日存入银行60 000元,年利率为2.00%,存款到期日即2000年1月1日将存款全部取出,国家规定凡1999年11月1日后孳生的利息收入应缴纳利息税,税率为20%,则该储户实际提取本金合计为_____。
A: 61 200元 B: 61 160元C: 61 000元 D: 60 040元
参考答案: B
33、某天办公桌上台历显示的是一周前的日期,将台历的日期翻到今天,正好所翻页的日期加起来是168,那么今天是几号?_____
A: 20B: 21C: 27D: 28
参考答案: D 本题解释:正确答案是D考点数列问题解析一周的日期成等差数列,则中位数为168÷7=24,因此这一周的日期分别为21、22、23、24、25、26、27,因此今天是28号。故正确答案为D。
34、连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,则正八面体的体积为_____立方厘米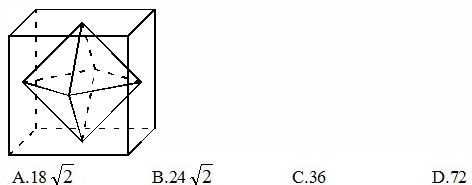
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
35、一杯含盐 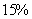 的盐水
的盐水 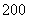 克,要使盐水含盐
克,要使盐水含盐 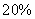 ,应该加盐多少克?_____
,应该加盐多少克?_____
A: 12.5B: 10C: 5.5D: 5
参考答案: A 本题解释:参考答案:A题目详解:应用工程法:设需要盐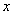 克,
克,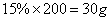 ;
;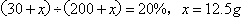 ;所以,选A。考查点:数量关系>数学运算>浓度问题>溶质变化
;所以,选A。考查点:数量关系>数学运算>浓度问题>溶质变化
36、建华中学共有1600名学生,其中喜欢乒乓球的有1180人,喜欢羽毛球的有1360人,喜欢篮球的有1250人,喜欢足球的有1040人,问以上四项球类运动都喜欢的至少有几人?_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:正确答案是B考点抽屉原理问题解析采取逆向思维法。不喜欢乒乓的1600-1180=420,不喜欢羽毛球的1600-1360=240,不喜欢篮球的1600-1250=350,不喜欢足球的1600-1040=560,要使四项运动都喜欢的人数最少,那么不喜欢的人数就要最多那么都尽量不相交,从而达到最多:420+240+350+560=1570人,所以喜欢的最少的为1600-1570=30人,故正确答案为B。
37、两枚导弹相距41620公里,处于同一弹道上彼此相向而行。其中一枚以每小时38000公里的速度行驶。另一枚以时速22000公里的速度行驶。问它们在碰撞前1分钟时相距多远?_____
A: 4.162公里B: 41.62公里C: 1000公里D: 60000公里
参考答案: C 本题解释:正确答案是C考点行程问题解析38000+22000=60000(公里/小时)=1000(公里/分钟),可见两个相对飞行的导弹以每分钟1000公里的速度靠近。那么,当它们在最后一分钟的时候,两者相距1000公里,故正确答案为C。
38、小明前三次数学测验的平均分数是88分,要想平均分数达到90分以上,他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。 分,该数值可以根据以上式子判定尾数为6,选择B。
分,该数值可以根据以上式子判定尾数为6,选择B。
39、_____ 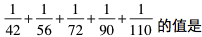
A: 1/6B: 5/66C: 7/85D: 1/128
参考答案: B 本题解释:正确答案是B考点计算问题解析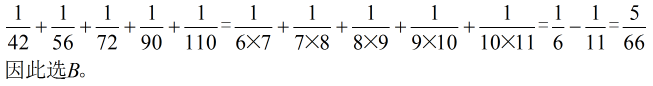
40、在1000以内,除以3余2,除以7余3,除以11余4的数有多少个?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:正确答案是B考点余数与同余问题解析同余问题,不符合“余同取余,和同加和,差同减差,最小公倍数做周期”的口诀,通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17,其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意:0≤231n+59≤1000,解得0≤n≤4。所以这样的数共有5个,故正确答案为B。口诀解释:余同取余,例如“一个数除以7余1,除以6余1,除以5余1”,可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如“一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如“一个数除以7余3,除以6余2,除以5余1”,可见除数与余数的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。
41、某月刊每期定价5元。某单位一部分人订半年,另一部分人订全年,共需订费480元;如果订半年的改订全年,订全年的改订半年,那么共需420元。共有多少人订了这份期刊?
A: 25B: 20C: 15D: 10
参考答案: D 本题解释:D。所有人订一年半期刊所花的钱为(480+420)元,则订了这份期刊的人数为(480+420)+[5×(6+12)]=10个人。
42、_____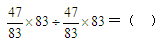
A: 1B: 83C: 2209D: 6889
参考答案: D 本题解释:正确答案是D考点计算问题解析
43、有41个学生要坐船过河,渡口处只有一只能载4人的小船(无船工),他们要全部渡过河去,至少要使用这只小船渡河多少次?_____
A: 23B: 24C: 27D: 26
参考答案: C 本题解释:【答案】C。解析:套用公式,过河次数=(41-1)/(4-1)=13.33,过河次数为整数,13<13.33<14,要使所有人都过河,只能取14。所求次数为单程次数,来回总共14×2-1=27次(最后一次过河不再返回)。故正确答案为C。公式:过河问题中每次过河都需要有一个人将船划回来,而最后一次过河不再需要划回来。N个人过河,船最多载M人,则过河次数为(N-1)/(M-1)。过河次数指单程次数,注意最后一次过河不需要人划回来,总次数=单程次数×2-1。
44、某单位有52人投票,从甲、乙、丙三人中选出一名先进工作者。在计票过程中的某时刻,甲得17票,乙得16票,丙得11票,如果规定得票比其他两人都多的候选人才能当选。那么甲要确保当选,最少要再得票_____。
A: 1张B: 2张C: 3张D: 4张
参考答案: D 本题解释:正确答案是D考点抽屉原理问题解析解析1:整体考虑,乙对甲威胁最大,甲乙共可以分52-11=41张选票,甲乙均得到20张时,甲仍然保证不了能当选,再得剩下的1张选票,即甲得到21张选票时,保证当选,所以还需要21-17=4张,选D。解析2:还剩下52-17-16-11=8张票。甲如果要确保当选,则考虑最差情况,剩下的票丙一票不拿,那么只有甲乙分配剩下的票,甲至少要拿8÷2=4张才能保证当选,故正确答案为D。解析3:已统计选票17+16+11=44,剩余52-44=8票。这里对甲最大的威胁是乙,设甲再得票x,乙再得票(8-x),令17+x=16+(8-x),由此推出,x=3.5,x最小是3.5,满足条件的整数取4,故正确答案为D。
45、两根同样长的蜡烛,点完粗蜡烛要3小时,点完细蜡烛要1小时。同时点燃两根蜡烛,一段时间后,同时熄灭,发现粗蜡烛的长度是细蜡烛的3倍。问两根蜡烛燃烧了多长时间?_____
A: 30分钟B: 35分钟C: 40分钟D: 45分钟
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析
46、牧场上一片青草,每天牧草都匀速生长。这片牧草可供10头牛吃20天,或者可供15头牛吃10天。问:可供25头牛吃几天?_____
A: 5B: 10C: 15D: 20
参考答案: A 本题解释:A【解析】 这类题难就难在牧场上草的数量每天都在发生变化,我们要想办法从变化当中找到不变的量。总草量可以分为牧场上原有的草和新生长出来的草两部分。牧场上原有的草是不变的,新长出的草虽然在变化,因为是匀速生长,所以这片草地每天新长出的草的数量相同,即每天新长出的草是不变的。下面,就要设法计算出原有的草量和每天新长出的草量这两个不变量。设1头牛一天吃的草为1份。那么,10头牛20天吃200份,草被吃完;15头牛10天吃150份,草也被吃完。前者的总草量是200份,后者的总草量是150份,前者是原有的草加 20天新长出的草,后者是原有的草加10天新长出的草。200-150=50(份),20-10=10(天),说明牧场10天长草50份,1天长草5份。也就是说,5头牛专吃新长出来的草刚好吃完,5头牛以外的牛吃的草就是牧场上原有的草。由此得出,牧场上原有草(l0-5)× 20=100(份)或(15-5)×10=100(份)。现在已经知道原有草100份,每天新长出草5份。当有25头牛时,其中的5头专吃新长出来的草,剩下的20头吃原有的草,吃完需100÷20=5(天)。所以,这片草地可供25头牛吃5天。因此,正确答案为A。
47、一个两位数的中间再加上一个0,那么所得的这个数是原数的9倍,原来这个两位数是多少?_____
A: 15B: 25C: 35D: 45
参考答案: D 本题解释:正确答案是D考点计算问题解析解析1:设这个两位数个位是x,十位是y,则100y+x=9(10y+x),4x=5y,符合要求的个位数x只有5,所以y=4,所以结果为45。解析2:四个选项直接代入,只有D符合要求。所以正确答案为D。秒杀技根据整除特性,一个数如果是9的倍数,那么这个数各位相加也是9的倍数。而插入的是0,所以原两位数各位相加也是9的倍数,只有D符合。标签直接代入数字特性
48、如果l※4=1234,2※3=234,7※2=78,那么4※5=_____。
A: 456B: 45678C: 5678D: 56789
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可得:1※4表示从1开始的4个连续自然数,即为1234;同理2※3表示从2开始的3个连续自然数,即为234;7※2表示从7开始的2个连续自然数,即为78;所以4※5表示的是从4开始的5个连续自然数,即为45678。所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
49、某单位共有职工72人,年底考核平均分数为85分,根据考核分数,90分以上的职工评为优秀职工,已知优秀职工的平均分为92分,其他职工的平均分数是80分,问优秀职工的人数是多少?_____
A: 12B: 24C: 30D: 42
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:假定优秀职工为X,其他职工为Y,则可得:X+Y=72,92X+80Y=85×72。解得X=30、Y=42。故正确答案为C。秒杀技观察选项C和D,二者选项相加为72,为待选选项。所有职工的平均分为85,显然更靠近80,则说明其他职工多于优秀员工,可确定优秀员工为30人。
50、某洗车店洗车分外部清洁和内部清洁,两道工序时间均不少于30分钟,而且同一辆车两道工序不能同时进行,洗车间同一时间只能容下2辆车。现有9辆车需要清洗,汽车进出洗车间的时间可忽略不计,则洗完9辆车至少需要的时间为_____。
A: 330分钟B: 300分钟C: 270分钟D: 250分钟
参考答案: C 本题解释:正确答案是C考点统筹规划问题解析前6辆车都是2辆车同时依次进行外部清洁和内部清洁,耗时60×3=180分钟。最后3辆车记为A、B、C,工作安排为A、B车外部清洁,然后B、C车内部清洁,然后A车内部清洁的同时C车外部清洁,共计耗时90分钟。因此洗完9辆车至少需要270分钟。故正确答案为C。
51、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇? _____
A: 8点48分B: 8点30分C: 9点D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
52、科学家对平海岛屿进行调查,他们先捕获30只麻雀进行标记,后放飞,再捕捉50只,其中有标记的有10只,则这一岛屿上的麻雀大约有_____。
A: 150只B: 300只C: 500只D: 1500只
参考答案: A 本题解释:正确答案是A考点概率问题解析假设岛上有X只麻雀,捕捉30只进行标记,再捕捉50只,其中有10只有标记,则可列等式X∶30=50∶10,X=1500÷10=150(只),故正确答案为A。
53、田忌与齐威王赛马并最终获胜被传为佳话,假设齐威王以上等马、中等马和下等马的固定程序排阵,那么田忌随机将自己的三匹马排阵时,能够获得两场胜利的概率是_____。
A: 2/3B: 1/3C: 1/6D: 1/9
参考答案: C 本题解释:正确答案是C考点概率问题解析 故正确答案为C。
故正确答案为C。
54、工作人员做成了一个长60厘米,宽40厘米,高22厘米的箱子,因丈量错误,长和宽均比设计尺寸多了2厘米,而高比设计尺寸少了3厘米,那么该箱子的表面积与设计时的表面积相差多少平方厘米?_____
A: 4B: 20C: 8D: 40
参考答案: C 本题解释:正确答案是C考点几何问题解析实际表面积为(60×40+40×22+60×22)×2,设计表面积为(58×38+38×25+58×25)×2,计算尾数,实际表面积尾数为0,设计表面积尾数为(4+0+0)×2=8,二者之差尾数为2或8,显然只有C符合条件。故正确答案为C。
55、n为100以内的自然数,那么能令2n-1被7整除的n有多少个?_____
A: 32B: 33C: 34D: 35
参考答案: B 本题解释:答案:B.[解析]当n是3的倍数的时候,2n-1是7的倍数。也就是求100以内3的倍数,从3到99,共有33个。故选B。
56、一桶农药,加入一定量的水稀释后,浓度为15%;再加入同样多的水稀释,农药的浓度变为12%,若第三次再加入同样多的水,农药的浓度将变为多少?_____
A: 8%B: 10%C: 11%D: 13%
参考答案: B 本题解释:B。【解析】设δ加水稀释前农药量为x,?次所加水量为a,所求浓度为y%,则(x+a)15%=(x+2a)12%=(x+3a)y%,解得y%=10%。
57、某企业调查用户从网络获取信息的习惯,问卷回收率为90%,调查对象中有179人使用搜索引擎获取信息,146人从官方网站获取信息,246人从社交网站获取信息,同时使用这三种方式的有115人,使用其中两种的有24人,另有52人这三种方式都不使用,问这次调查共发出了多少份问卷:_____
A: 310B: 360C: 390D: 410
参考答案: D 本题解释:正确答案是D,解析:根据题意,收回问卷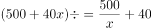 ,则所求为
,则所求为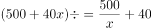 。故正确答案为D。考点:容斥原理问题
。故正确答案为D。考点:容斥原理问题
58、三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数_____。
A: 48人B: 49人C: 50人D: 51人
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析解析1:设甲单位的人数为x人,则乙单位的人数为(x+2)人,丙单位的人数为(x+x+2-20)即为(2x-18)人,根据题意可得:x+(x+2)+(2x-18)=180,解得x=49,故选择B选项。解析2:由“三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人”可得甲、乙两单位人数之和为:(180+20)÷2=100,又知“甲单位比乙单位少2人”,因此甲单位人数为:(100-2)÷2=49,故选择B选项。故正确答案为B。
59、三种动物赛跑,已知狐狸的速度是兔子的2/3,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑_____米。
A: 28B: 14C: 19D: 7
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析根据题意,设兔子、狐狸、松鼠的速度比为6:4:3,一分钟松鼠比狐狸少跑14米,说明一份为14米/分钟,所以兔子和狐狸的速度分别为6×14和4×14,因此半分钟兔子比狐狸多跑(6×14-4×14)÷2=14米,故正确答案为B。秒杀技题目中时间为半分钟,实际上是一个时间陷阱,根据猜题技巧,选项中应有一个干扰选项是正确选项的2倍,只有A、B符合,即B项正确。标签猜题技巧
60、(浙江2002,第14题)下列选项中,值最小的是_____。
A: 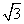 B:
B: 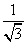 C:
C: 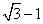 D:
D: 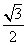
参考答案: B 本题解释:参考答案:B题目详解:观察选项可知: ,
, ;我们从简单着手,很明显可得到:
;我们从简单着手,很明显可得到: ,排除A、D选项;再比较
,排除A、D选项;再比较 和
和 的大小:
的大小: ,
, ,所以
,所以 ,排除C选项;所以,选B。解法二:遇到类似问题我们还可以采用“平方法”来比较大小。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
,排除C选项;所以,选B。解法二:遇到类似问题我们还可以采用“平方法”来比较大小。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
61、有甲、乙两个项目组。乙组任务临时加重时,从甲组抽调了四分之一的组员。此后甲组任务也有所加重,于是又从乙组调回了重组后乙组人数的十分之一。此时甲组与乙组人数相等。由此可以得出结论_____。
A: 甲组原有16人,乙组原有11人B: 甲、乙两组原组员人数之比为16∶11C: 甲组原有11人,乙组原有16人D: 甲、乙两组原组员人数比为11∶16
参考答案: B 本题解释:答案:B。设甲组原有a人,乙组原有b人,故由题意可得:(b+a/4)×9/10=1/10(b+a/4)+3/4a,所以
A:b=16:11。
62、 _____
_____
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析将各项直接代入检验,只有B项符合,(21-5)/(29-5)=16/24=2/3,故正确答案为B。标签直接代入
63、(2009•国考)甲、乙两人共有260本书,其中甲的书有13%是专业书,乙的书有12.5%是专业书,问甲有多少本非专业书?_____
A: 75B: 87C: 174D: 67
参考答案: B 本题解释:参考答案:B本题得分:题目详解:根据题意甲的专业书:甲的书有13%是专业书,即有甲的13/100是专业书;甲的书本数:由于书的本数为整数,则甲的书本数只能为100或200;乙的专业书:乙的书有12.5%是专业书,即有乙的1/8是专业书;乙的书本数:由于书的本数为整数,则乙的书本数必能被8整除;甲、乙两人共有260本书,甲的书本数为100或200,则乙的书的本数为160或60,其中只有160能被8整除,故乙的书本数为160,则甲有100本书,其非专业书本数为100×(1-13%)=87本。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
64、某公司中午订餐,周一有27人订餐,周二有39人订餐,周三有43人订餐,周四有41人订餐,周五有39人订餐。如果在这五天至少有一天订餐的人有39人,那么五天都订餐的最多有多少人?_____
A: 27B: 26C: 25D: 24
参考答案: A 本题解释:参考答案:A题目详解:依题意:将39人分为仅订餐一次和五天都订餐的;那么五天都订餐的最多有: 人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
65、
66、甲、乙、丙、丁四人,其中每三个人的岁数之和分别是55、58、62、65。这四个人中年龄最小的是_____。
A: 7岁B: 10岁C: 15岁D: 18岁
参考答案: C 本题解释:正确答案是C考点平均数问题解析将55、58、62、65直接相加,可知其值等于原来四个数之和的3倍,于是可知原四个数字之和为(55+58+62+65)÷3=80,因此最小的数为80-65=15。故正确答案为C。
67、小王去一个离家12千米的地方,他每小时步行3千米,每步行50分钟他要休息10分钟,8点整出发,他几点可以到目的地?_____
A: 12点B: 12点30分C: 12点35分D: 12点40分
参考答案: D 本题解释:D。小王不休息的话他走12千米所需的时间是12÷3=4(小时),4小时包含4个50分钟余40分钟,因此小王总共休息了4个10分钟,那么小王花费的总时间是4小时40分钟,也就是小王到达目的地的时间是12点40分。故选D。名师点评:本题很多考生会有如下解法:根据题意每小时中有50分钟行走、10分钟休息,则每个小时小王实际行进2.5千米,因此要步行12千米,用时为12÷2.5=4.8(小时),合4小时48分钟。这是一种典型的错误解法,因为这样相当于取的是等价速度,在整数小时部分不会出现错误,但在非整数部分也即在最后一段,并不是按等价速度来行进的,而是直接行进40分钟到达目的地,而无休息时间。
68、某次数学竞赛设一、二等奖。已知(1)甲、乙两校获奖的人数比为 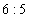 。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的
。(2)甲、乙两校获二等奖的人数总和占两校获奖人数总和的 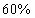 。(3)甲、乙两校获二等奖的人数之比为
。(3)甲、乙两校获二等奖的人数之比为 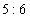 。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
。问甲校获二等奖的人数占该校获奖总人数的百分数是几?_____
A: 20B: 30C: 50D: 60
参考答案: C 本题解释:参考答案:C题目详解:已知甲、乙两校获二等奖的人数之比为5:6,那么设甲获二等奖的人数为5份,乙为6份。因为二等奖的人数占两校人数总和的60%,那么甲校获二等奖人数占总数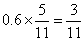 又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的
又因为甲、乙两学校获奖人数比为6:5,所以设总人数为11份,甲得奖的占其中6份可知甲校获二等奖者占该校获奖总人数的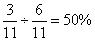 。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
。所以,选C。考查点:数量关系>数学运算>和差倍比问题>比例问题
69、工人甲一分钟可生产螺丝3个或螺丝帽9个,工人乙一分钟可生产螺丝2个或螺丝帽7个,现在两人各花20分钟,共生产螺丝和螺丝帽134个,问生产的螺丝比螺丝帽多几个?_____
A: 34个B: 32个C: 30个D: 28个
参考答案: A 本题解释:正确答案是A考点不定方程问题解析设两人20分钟全部生产螺丝,则共生产了100个,注意到甲生产螺帽比螺丝每分钟多6个,乙每分钟多5个。设甲生产螺帽X分钟,乙生产螺帽Y分钟,根据鸡兔同笼原理,有6X+2Y=134-100,当X=4,Y=2时,符合条件,再代入计算,得螺帽有4×9+2×7=50个,螺丝有84个,则螺丝比螺帽多84-50=34个。故正确答案为A。
70、2005年7月1日是星期五,那么2008年7月1日是星期几_____
A: 星期三B: 星期四C: 星期五D: 星期二
参考答案: D 本题解释:正确答案是D考点星期日期问题解析2005,2006,2007都是平年(365天),2008是闰年(366天),365=52×7+1,所以,经历一个平年(365天),星期往后推一天,366=52×7+2,所以,经历一个闰年(366天),星期往后推两天,因为2005年7月1日是星期五,所以2008年7月1日是星期五+1+1+2=星期日+2=星期二。故正确答案为D。标签差异分析
71、某鞋业公司的旅游鞋加工车间要完成一出口订单,如果每天加工50 双,要比原计划晚3 天完成,如果每天加工60 双,则要比原计划提前2 天完成,这一订单共需要加工多少双旅游鞋?_____
A: 1200 双 B: 1300 双 C: 1400 双 D: 1500 双
参考答案: D 本题解释:【答案】D[解析]能被50、60整除的,排除B和C,再依次代入A和D,A不符合,所以选D。
72、把一个长18米、宽6米、高4米的大教室,用厚度为25厘米的隔墙将长分为3段,形成3个活动室(隔墙砌到顶),每间活动室的门窗面积都是15平方米,现在用石灰粉刷3个活动室的内墙壁和天花板,平均每平方米用石灰0.2千克,那么,一共需要石灰_____千克。
A: 68.8B: 74.2C: 83.7D: 59.6
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:天花板总面积是:(18-0.25×2)×6=105平方米,内壁总面积是:(18-0.25×2)×4×2+4×6×6-15×3=239平方米,需用石灰粉刷的总面积是:105+239=344平方米,需用石灰为:344×0.2=68.8千克。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
73、某车间从3月2日开始每天调入人,已知每人每天生产~件产品,该车间从月1日至3月21日共生产840个产品.该车间应有多少名工人? _____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:【答案】B。解析:从3月2日开始调入的每一个人生产的产品的个数正好组成以1为公差的等差数列20,19,18,……1,得调入的人生产的总产品数是:(20+1)×20÷2=210(个),所以原有工人生产的产品数=840-210=630(个),每人每天生产一个,所以工人数=630/21=30(个)。
74、在1至1000的1000个自然数中,既不是4的倍数,也不是6的倍数的数共有多少个?_____
A: 375B: 416C: 625D: 791
参考答案: C 本题解释:C【解析】1000÷4=250(个),所以1至1000中4的倍数的数有250个。1000÷6=166……4,所以1至1000中6的倍数的数有166个。1000÷(4×6)=41……16,说明1至1000中既是4的倍数,又是6的倍数的数有41个。即4的倍数的个数与6的倍数的个数的交集有41个,如图所示。所以1至1000中,既是4的倍数,也是6的倍数的数共有209+125+41=375(个)。则1至1000中,既不是4的倍数,也不是6的倍数的数共有:1000-(209+125+41)=1000-375=625(个)。故本题选C。
75、某公司的6名员工一起去用餐,他们各自购买了三种不同食品中的一种,且每人只购买了一份。已知盖饭15元一份,水饺7元一份,面条9元一份,他们一共花费了60元。问他们中最多有几人买了水饺?_____
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:正确答案是C考点不定方程问题解析假定购买三种食物人数分别为X、Y、Z,根据题意X+Y+Z=6,15X+7Y+9Z=60。要使得水饺最多,则其他尽可能少。根据奇偶性质,可知X、Y、Z三个数中必然两个为奇数一个为偶数,或者三个均为偶数。将选项代入验证,若Y=4,此时X、Z无正整数解;若Y=3,可知X=2,Z=1,符合题意。因此正确答案为C。秒杀技得到15X+7Y+9Z=60后,注意到15、9、60均能被3整除,因此7Y必然能被3整除,仅C符合。
76、在一只底面半径是20cm的圆柱形小桶里,有一半径为l0cm的圆柱形钢材浸没在水中,当钢材从桶中取出后,桶里的水下降了3cm。求这段钢材的长度。_____
A: 3cmB: 6cmC: 12cmD: 18cm
参考答案: C 本题解释:【答案】C。解析:钢材的体积与水下降的体积相等,钢材长度与水下降的高度之比等于二者底面积之比的倒数,由此可得钢材长度为3×4=12。
77、股票买入和卖出都需要通过证券公司进行交易,每次交易费占交易额的2‰。某人以10元的价格买入1000股股票,几天后又以12元的价格全都卖出,若每次交易还需付占交易额3‰的印花税,则此人将获利_____。
A: 1880元B: 1890元C: 1900元D: 1944元
参考答案: B 本题解释:正确答案是B考点经济利润问题解析交易两次,所以交两次交易费,交两次印花税,故可得如下:(12-10)×1000-(12+10)×1000×(2‰+3‰)=2000-22000×5‰=2000-110=1890,故正确答案为B。
78、篮球规则中得分有3分,2分,1分,若在一次比赛中,队员A一人得了13分,那么他的得分组合共_____种。
A: 18 B: 19 C: 20 D: 21
参考答案: D 本题解释:D[解析]当A的3分分别拿到4,3,2,1,0次的时候,对应的组合数分别是1,3,4,6,7,所以A的得分组合共有1+3+4+6+7=21种,选D。
79、公路上有三辆同向行驶的汽车,其中甲车的时速为63公里,乙、丙两车的时速均为60公里,但由于水箱故障,丙车每连续行驶30分钟后必须停车2分钟。早上10点,三车到达同一位置,问1小时后,甲、丙两车最多相距多少公里?_____
A: 5B: 7C: 9D: 11
参考答案: B 本题解释:正确答案是B考点行程问题解析在这1个小时中,丙车最多休息4分钟,也即丙在一个小时内最少行程为60×56÷60=56公里。而甲车持续行驶,可达63公里。因此两车最多相距7公里,故正确答案为B。
80、地上放着一个每一面上都有一个数的六面体箱子,对面两个数的和均为27,甲能看到顶面和两个侧面,这三个面上的数字之和是35;乙能看到顶面和另外两个侧面,且这三个面上的数字和为47。箱子贴地一面的数字是_____。
A: 14B: 13C: 12D: 11
参考答案: B 本题解释:正确答案是B考点趣味数学问题解析题目给出对面数字之和为27,则注意将其余条件中出现的对面合在一起。从这一点出发,可以看出若将甲与乙看到的面合在一起,则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面,也即其数字之和为27×2=54,因此顶面的数字为(35+47-54)÷2=14,于是底面数字为27-14=13,故正确答案为B。
81、李先生去10层楼的8层去办事,恰赶上电梯停电,他只能步行爬楼。他从第1层爬到第4层用了48秒,请问,以同样的速度爬到第8层需要多少秒? _____
A: 112B: 96C: 64D: 48
参考答案: A 本题解释:A【解析】假设每上一层楼的路程为一段楼梯,李先生从第1 层爬到第4 层,路程为3 段楼梯,用时48 秒,则每一段楼梯用时16 秒,第1 层到第8 层路程为7 段,则需用时16×7=112 秒。故选A。
82、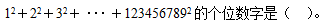 _____
_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:正确答案是C考点计算问题解析
83、有A、B两种商品,如果A的利润增加20% ,B的利润减少10% ,那么A、B两商品的利润就相同了。问原来A商品的利润是B商品利润的百分之几?_____
A: 80%B: 70%C: 85% D: 75%
参考答案: D 本题解释:D
84、出租车在7公里以内收费10.6元(不足7公里按7公里收费),以后每走1公里收费1.8元,某乘客有一次乘出租车花了34元,他乘坐了多少公里?_____
A: 16B: 17C: 20D: 23
参考答案: C 本题解释:C解析:设他乘坐了x公里,根据题意列方程,得:10.6+(x-7)×1.8=34,解得:x=20,选C。
85、某市规定,出租车合乘部分的车费向每位乘客收取显示费用的60%,燃油附加费由合乘客人平摊。现有从同一地方出发的三位客人合乘,分别在D、E、F点下车,显示的费用分别为10元、20元、40元,那么在这样的合乘中,司机的营利比正常(三位客人是一起的,只是分别在上述三个地方下车)多_____。
A: 1元B: 2元C: 10元D: 12元
参考答案: C 本题解释:正确答案是C考点分段计算问题解析第一位下车客人为合乘,涉及金额为10元;第二位下车客人为合乘,涉及金额为20元;第三位下车客人合乘部分涉及金额20元,独乘部分涉及金额为20元;所以实际营利为10×60%+20×60%+20×60%+20=50元,比正常多50-40=10元。故正确答案为C。标签分类分步
86、父亲和儿子的年龄和为50岁,三年前父亲的年龄是儿子的三倍,多少年后儿子年满18岁?_____
A: 2B: 4C: 6D: 8
参考答案: 本题解释:B【解析】设x年后儿子年满18岁,则儿子现在的年距为18-x,父亲为50-(18-x)=32+x,根据题意得:3(18-x-3)=32+x-3,解得x=4,故正确答案为B。
87、甲、乙、丙、丁四人做手工纸盒,已知甲、乙、丙三人平均每人做了28个,乙、丙、丁三人平均每人做了31个,已知丁做了33个,问甲做了多少个?_____
A: 24个B: 26个C: 27个D: 28个
参考答案: A 本题解释:正确答案是A考点平均数问题解析由题意,甲、乙、丙共做了28×3=84个,乙、丙、丁共做了31×3=93个,则丁比甲多做了93-84=9(个),已知丁做了33个,那么甲做了33-9=24个,故正确答案为A。
88、小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇。问他们两人第四次相遇的地点离乙村多远(相遇指迎面相遇)?_____
A: 1千米 B: 1.2千米C: 1.5千米D: 1.8千米
参考答案: A 本题解释:【答案】A。解析:直线多次相遇问题。第二次相遇两人已共同走了甲、乙两村距离的3倍,因此张走了3.5×3=10.5千米。从图上可看出,第二次相遇处离乙村2千米,因此,甲、乙两村距离是10.5-2=8.5千米。每次相遇甲乙二人路程和都比上次相遇多2倍的两地间距。第四次相遇时,两人已共同走了(3+2+2)倍的两村距离,其中张走了3.5×(2×4-1)=24.5千米,24.5=8.5+8.5+7.5千米。因此第四次相遇处,离乙村8.5-7.5=1千米。
89、“红星”啤酒开展“7个空瓶换l瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期问共喝掉347瓶“红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296B: 298C: 300D: 302
参考答案: B 本题解释:由题可知,6个空瓶可以换一个瓶子里面的啤酒,298÷6=49……4,只有49+298=347。
90、如果当“张三被录取的概率是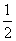 ,李四被录取的概率是
,李四被录取的概率是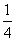 时,命题:要么张三被录取,要么李四被录取”的概率就是_____
时,命题:要么张三被录取,要么李四被录取”的概率就是_____
A: 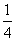 B:
B: 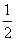 C:
C: 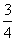 D:
D: 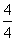
参考答案: B 本题解释:参考答案:B题目详解:“要么张三录取要么李四录取”就是:2人不能同时录取且至少有一人录取;张三被录取的概率是 ,李四被录取的概率是
,李四被录取的概率是 ;那么有两种情况:张三被录取但李四没被录取的概率:
;那么有两种情况:张三被录取但李四没被录取的概率: ;张三没被录取但李四被录取的概率:
;张三没被录取但李四被录取的概率: ;所以,概率为:
;所以,概率为: ;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选B。考查点:数量关系>数学运算>概率问题>条件概率
91、用a、b、c三种不同型号的客车送一批会议代表到火车站,用6辆a型车,5趟可以送完;用5辆a型车和10辆b型车,3趟可以送完;用3辆b型车和8辆c型车,4趟可以送完。问先由3辆a型车和6辆b型车各送4趟,剩下的代表还要由2辆c型车送几趟?_____
A: 3趟B: 4趟C: 5趟D: 6趟
参考答案: B 本题解释:【答案】B。解析:方程法解题,主要求出a=2b,3b=2c,然后列方程求得选择B选项。
92、甲、乙两人玩打赌游戏,连续抛三个硬币,如果同时出现正面或同时出现反面算乙输,出现两个正面或两个反面算甲输,若甲输,则甲要给乙10元,问:乙输要给甲多少,甲才肯玩游戏?_____
A: 10元B: 15元C: 20元D: 30元
参考答案: D 本题解释:参考答案 题目详解:连续抛三个硬币,同时出现正面或反面的概率是:
题目详解:连续抛三个硬币,同时出现正面或反面的概率是: 即
即 ;出现两个正面或两个反面的概率是:
;出现两个正面或两个反面的概率是: 即
即 ;可见甲输的概率是乙输的概率的3倍;因此乙若输,则需要给甲
;可见甲输的概率是乙输的概率的3倍;因此乙若输,则需要给甲 (元),甲才肯玩这个游戏;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
(元),甲才肯玩这个游戏;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
93、有一列车从甲地到乙地,如果是每小时行100千米,上午11点到达,如果每小时行80千米是下午一点到达,则该车的出发时间是_____
A: 上午7点 B: 上午6点 C: 凌晨4点 D: 凌晨3点
参考答案: D 本题解释: 【解析】D。设出发时间是T,那么100×(11-T)=80(13-T),解得T=3,即凌晨3点。
94、甲班与乙班同学同时从学校出发去某公园,甲班步行的速度是每小时4千米,乙班步行的速度是每小时3千米。学校有一辆汽车,它的速度是每小时48千米,这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达,那么,甲班学生与乙班学生需要步行的距离之比是_____。
A: 15:11B: 17:22C: 19:24D: 21:27
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析设甲步行X小时,乙步行Y小时。故可得方程4X+48Y=3Y+48X,解得X:Y=45:44,所以步行距离之比4X:3Y=15:11,故正确答案为A。
95、用方形地砖铺一块了正方形地面,四周用不同颜色的地砖加以装饰,用47块不同颜色的砖装饰了这块地面相邻的两边。这块地面一共要用_____块砖。
A: 324B: 576C: 891D: 1024
参考答案: B 本题解释:B【解析】最外层每边铺地砖(47+1)÷2=24块,故一共要用24×24=576块砖。
96、一个边长为20的方阵,最外面三圈人数总和为多少?_____
A: 196B: 204C: 256D: 324
参考答案: B 本题解释:参考答案:B题目详解:方阵边长为20,总人数为400;除去最外面三圈人数,里面的小方阵边长为: ,人数为
,人数为 ;最外面三圈人数为:
;最外面三圈人数为: 人。所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
人。所以,选B。考查点:数量关系>数学运算>特殊情境问题>方阵问题>空心方阵问题
97、3种动物赛跑,已知狐狸的速度是兔子的 ,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑_____米。
A: 28B: 19C: 14D: 7
参考答案: C 本题解释:C【解析】由题意可得:兔子速度∶松鼠速度∶狐狸速度=6∶3∶4,又因为“一分钟松鼠比狐狸少跑14米”即半分钟松鼠比狐狸少跑7米,所以令半分钟兔子、松鼠、狐狸分别跑6a、3a、4a,4a-3a=7,故a=7,所以半分钟兔子比狐狸多跑6×7-4×7=14(米)。
98、小蔡去超市购物,她买了1.6千克苹果,4磅食油和3.8市斤芦柑。请问小蔡买的这三种食品最重的是哪一种?_____
A: 苹果B: 食油C: 芦柑D: 三者一样重
参考答案: C 本题解释:正确答案是C考点其他解析本题主要考查不同单位之间的数量比较,做此类题目,应首先换算为同一单位。1磅=0.454千克,1市斤=0.5千克,故:4磅=1.816千克,3.8市斤=1.9千克,所以1.6<1.816<1.9,故正确答案为C。
99、某月的最后一个星期五是这个月的25号,这个月的第一天是星期几?_____
A: 星期二B: 星期三C: 星期四D: 星期六
参考答案: A 本题解释:A 【解析】因为25=3×7+4,所以这个月的4号也是星期五,故这个月的第一天是星期二。
100、杯中原有浓度为18%的盐水溶液100ml,重复以下操作2次,加入100ml水,充分配合后,倒出100ml溶液,问杯中盐水溶液的浓度变成了多少?_____
A: 9%B: 7.5%C: 4.5%D: 3.6%
参考答案: C 本题解释:第一次操作后盐水浓度为 ,第二次操作后浓度为
,第二次操作后浓度为 ,故应选择C。
,故应选择C。