时间:2016-06-16 22:15:14
1、一学校的750名学生或上历史课，或上算术课，或两门课都上。如果有489名学生上历史课，606名学生上算术课，问有多少学生两门课都上?_____。
A: 117B: 144C: 261D: 345
参考答案: D 本题解释:参考答案
题目详解:解法一：设两门课都上的学生有x人。
(原因:因为学数学的和学历史的人数和为1095人，但是全年级只有750人，这就说明有一部分同学是两科都学的，也就把两科都学的人算了两遍，所以只要减去年级总人数，剩下的就是两科都学的人数。)解法二：解设两门都上的人有
人，只学数学的人有
人，只学历史的人有
人。
①
②
③1-②得，
把代入③中，得
。所以，选D。解法三：直接用尾数法快解，秒杀题。
，尾数为5的只有D。(该解析由用户“估计考不上”于2010-12-0213:04:48贡献，感谢感谢!)考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
2、现有50名学生都做物理、化学实验，如果物理实验做正确的有40人，化学实验做正确的有31人，两种实验都做错的有4人，则两种实验都做对的有_____。
A: 27人B: 25人C: 19人D: 10人
参考答案: B 本题解释:参考答案:B题目详解:解法一：A={{物理实验做正确的人}};B={{化学实验做正确的人}}
={{至少做对一种的人数}};
={{两种实验都做对的人}}根据容斥原理可得：
，代入得：
。则
，所以，选B。解法二：由题意知，两种试验都做错的有4人，则至少做对一种的有46人。而题目已经告知有40人做对物理实验，则说明有6人只做对化学试验。同时有31人作对化学试验，则说明有15人只做对物理实验而做错了化学实验。所以题目的解答为:50-4(全做错)-15(物理对化学错)-6(化学对物理错)=25人。所以，选B。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
3、如右图，三个图形共覆盖的面积为290，其中X、Y、Z的面积分别为64、180、160。X与Y、Y与Z、Z与X的重叠面积分别为24、70、36，求阴影部分面为_____。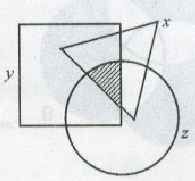
A: 12B: 16C: 18D: 20
参考答案: B 本题解释:参考答案:B题目详解:由题意可知，假设阴影部分面积为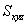
，设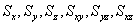
分别为相对应X、Y、Z、XY重叠部分、YZ重叠部分、XZ重叠部分的面积，则覆盖住桌面的总面积为：
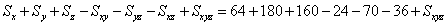解得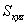
=16。(注意利用尾数法简便计算)。所以，选B考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
4、开运动会时，高一某班共有28名学生参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳和田径比赛的有3人，同时参加游泳和球类比赛的有3人，没有人同时参加三项比赛。问同时参加田径和球类比赛的有多少人?_____
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:参考答案:C题目详解:解法一：根据题意，设：参加游泳为
，参加田径为
，参加球类为
，参加游泳和田径比赛的为
，参加游泳和球类比赛的为
，参加三项比赛的为
，所求参加田径和球类比赛的为：
;由三个集合的容斥原理可以得到，同时参加田径和球类比赛的有：
人。解法二：设同时参加田径和球类比赛共有
人，参加游泳为，参加田径为，参加球类为，由“容斥原理”构建方程有：
，解得=3。因此，同时参加田径和球类比赛共有3。所以，选C。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
5、(2007国家，第55题)一名外国游客到北京旅游，他要么上午出去游玩，下午在旅馆休息，要么上午休息，下午出去游玩，而下雨天他只能一天都待在屋里。期间，不下雨的天数是12天，他上午待在旅馆的天数为8天，下午待在旅馆的天数为12天，他在北京共待了多少天?_____
A: 16天B: 20天C: 22天D: 24天
参考答案: A 本题解释:参考答案:A题目详解:解法一：设这个人在北京共待了n天，其中12天不下雨，那么n-12天下雨。根据公式“上午待在旅馆的天数+下午待在旅馆的天数-上下午都待在旅馆的天数(就是下雨的天数)=总天数-上下午都不待在旅馆的天数(根据题意不存在这样的一天)”可得：8+12-(n-12)=n-0，解得n=16。解法二：设游客在京期间下雨天数为x。因为他上午待在旅馆的8天中包括两部分：因下雨无法出去的天数(x)和因下午出去游玩而休息的天数(8-x);同理，下午待在旅馆的12天中包括两个部分：因下雨无法出去的部分(x)和因上午出去游玩而休息的部分(12-x)。由题意可得：(8-x)+(12-x)=12解得x=4，所以一共在北京待了16天。所以，选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
6、学校文艺组每人至少会演奏一种乐器，已知会拉手提琴的有24人，会弹电子琴的有17人，其中两样都会的有8人。这个文艺组一共有多少人?_____
A: 25B: 32C: 33D: 41
参考答案: C 本题解释:参考答案:C题目详解:根据题意，设：A={{会拉手风琴的}}，B={{会弹电子琴的}}，因此
={{文艺组的人}}，
={{两样都会的}}，由两个集合的容斥原理可得：
=
。所以，选C。考查点:数量关系>数学运算>容斥原理问题>两个集合 容斥关系
7、(2005国家一类，第45题)对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛，38人喜欢看戏剧，52人喜欢看电影，既喜欢看球赛又喜欢看戏剧的有18人，既喜欢看电影又喜欢看戏剧的有16人，三种都喜欢看的有12人，则只喜欢看电影的有多少人?_____
A: 22人B: 28人C: 30人D: 36人
参考答案: A 本题解释:参考答案:A题目详解:解法一：将题目条件代入下面三集合文氏图，凭借各部分加减关系依次标上相应数据：
我们看最后一个图：三个圆一共是100人，除去“喜欢球赛”的58个人，从图中可以看出只剩下三部分的人数应该为
人。而这三部分有两部分在图中已经标出分别为4人和16人，所以最后一部分“只喜欢电影”的人数应该是42-20=22人解法二：本题可以利用“两集合标准型核心公式”直接计算，根据公式“喜欢看球赛的人数+喜欢看戏剧的人数-既喜欢看球赛又喜欢看戏剧的人数=总数-既不喜欢看球赛又不喜欢看戏剧的人数”可得：
，解得，
。这22人既不喜欢看球赛又不喜欢看戏剧，就是只能喜欢看电影的人数了。解法三：根据题意，设既喜欢看电影又喜欢看球赛的为x人则有：
解得，
则只喜欢看电影的人为：
。所以，选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
8、(2008广东，第13题)60个人上身着白上衣或黑上衣，下身着蓝裤子或黑裤子。其中有12个人穿白上衣蓝裤子，有34个人穿黑裤子，有29个人穿黑上衣，求身着黑裤子黑上衣多少人?_____
A: 13B: 14C: 15D: 20
参考答案: C 本题解释:参考答案:C题目详解:解法一：根据题意，设穿黑裤子黑上衣的人数有x人。根据公式“黑裤子数+黑上衣数-黑裤子黑上衣数=总数-白衣服蓝裤子数”可得:
，解得
。所以，选C。解法二：根据题意，设上衣分别为1、2，裤子分别为3、4。总共4种穿衣的情况：
;
;又因为：
，
，
，
;所以，可得：
所以，选C。解法三：根据题意，可知：60名运动员中有34人穿黑裤子，则剩下的60-34=26人穿蓝色裤子。而穿蓝色裤子的26人中有12人穿白上衣，那么剩下的26-12=14人穿黑上衣且蓝裤子又穿黑上衣的29人中有14人穿蓝裤子，那么剩下的人穿黑裤子且黑上衣，有29-14=15人。如图所示：
所以，选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
9、某班参加体育活动的学生有25人，参加音乐活动的有26人，参加美术活动的有24人，同时参加体、音乐活动的有16人，同时参加音、美活动的有15人，同时参加美、体活动的有14人，三个组织都参加的有5人，这个班共有多少名学生参加活动?_____
A: 24B: 26C: 30D: 35
参考答案: D 本题解释:参考答案题目详解:典型的三个集合的容斥问题，参加体育活动的学生为
;参与音乐活动的学生为
;参与美术活动的学生为
;参与体、音活动的学生为
;参与音、美活动的学生为
;参与美、体活动的学生为
;三个组织都参加的学生为
;所要求的是
由三个集合的容斥原理可以得到，这个班参加活动的学生有
=
人。所以，选D考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
10、调查公司对甲、乙、丙三部电影的收看情况向125人进行调查，有89人看过甲片，47人看过乙片，63人看过丙片，24人三部都看过，20人一部也没有看过，问只有看过其中两部的有多少人?_____
A: 69B: 65C: 57D: 46
参考答案: D 本题解释:参考答案题目详解:考查文氏图运算。
甲乙丙中至少看过一部电影的有：
。假设只看过一部的有
人，只看过两部的有
人，则有：1
;1
。由①②可得：
，
，则只看过两部的有46人，所以，选D。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
11、实验小学举办学生书法展，学校的橱窗里展出了每个年级学生的书法作品，其中有28幅不是五年级的，有24幅不是六年级的，五、六年级参展的书法作品共有20幅。一、二年级参展的作品总数比三、四年级参展的作品总数少4幅。一、二年级参展的书法作品共有多少幅?_____
A: 6B: 10C: 16D: 20
参考答案: A 本题解释:参考答案:A题目详解:28幅不是五年级的，也就是六年级+其他年级=28幅;24幅不是六年级的，也就是五年级+其他年级=24幅;上述两个式子相加得：(五年级+六年级)
其他年级
，因此，其他年级的=
幅;又因一、二年级参展的作品总数比三、四年级参展的作品总数少4幅，因此一、二年级参展的书法作品共有
幅。所以，选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
12、(2006国考B类)某工作组有12名外国人，其中6人会说英语，5人会说法语，5人会说西班牙语;有3人既会说英语又会说法语，有2人既会说法语又会说西班牙语，有2人既会说西班牙语又会说英语;有1人这三种语言都会说。则只会说一种语言的人比一种语言都不会说的人多：_____
A: 1人B: 2人C: 3人D: 5人
参考答案: C 本题解释:参考答案:C题目详解:根据题意，设：
=会说英语的人=6，
=会说法语的人=5，
=会说西班牙语的人=5，
=会说英语和法语的人=3，
=会说法语和西班牙语的人=2，
=会说西班牙语和英语的人=2，
=三种语言都会说的人=1。根据题意，观察下边文氏图，可知，所求为：
。根据公式：
。因此，所求为：
。所以，选C。
按照题意依次填入图中数据，则可知：只会说一种外语的有
(人)，一种外语也不会的有2人，则只会说一种外语的比一种外语都不会说的多3人，所以，选C。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
13、五年级有122名学生参加语文、数学考试，每人至少有一门功课取得优秀成绩，其中语文成绩优秀的有65人，数学成绩优秀的有87人。语文、数学都优秀的有多少人?_____
A: 30B: 35C: 57D: 65
参考答案: A 本题解释:参考答案:A题目详解:此题是典型的两个集合的容斥问题，由题意设：A={{语文成绩优秀的人}};B={{数学成绩优秀的人}};因此，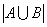
={{五年级参加语文、数学考试的人}};
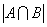={{语文和数学都优秀的人}}由两个集合的容斥原理可得：=
=
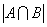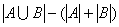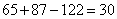所以，选A。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
14、(2008浙江)小明、小刚和小红三人一起参加一次英语考试，已知考试共有100道题，且小明做对了68题，小刚做对了58题，小红做对了78题。问三人都做对的题目至少有几题?_____
A: 4题B: 8题C: 12题D: 16题
参考答案: A 本题解释:参考答案:A题目详解:本题可以解读为：做错的题目最多会有多少道。小明答错的为32题，小刚答错的为42题，小红答错的为22题，当他们三人答错的题目各不相同的时候，错题的数量最大。所以错题最多是
道，也就是至少有100-96=4道题目是三人全对的。因此，选A。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系
15、(2005国家二类，第45题)外语学校有英语、法语、日语教师共27人，其中只能教英语的有8人，只能教日语的有6人，能教英、日语的有5人，能教法、日语的有3人，能教英、法语的有4人，三种都能教的有2人，则只能教法语的有多少人?_____
A: 4人B: 5人C: 6人D: 7人
参考答案: B 本题解释:参考答案:B题目详解:“由中间向外围”进行数据标记，进行简单加减运算，如下图过程所示：
[注释]本题中注意两个非常重要的要点：(1)题中表述的“只能教……”与其他题目可能存在的“能教……”是两个完全不同的概念，标数字的时候切记区别;(2)本题首句表明“这27个人中不存在三种语言都不教的人”，而其他一些题目可能存在三个条件都不满足的情形，计算的时候切记区别。考查点:数量关系>数学运算>容斥原理问题>三个集合容斥关系