时间:2016-06-16 21:52:45
1、小李开了一个多小时会议,会议开始时看了手表,会议结束时又看了手表,发现时针与分针恰好互换了位置。问这次会议大约开了1小时多少分?_____
A: 51B: 47C: 45D: 43
参考答案: A 本题解释:A。时针和分针正好互换了位置,说明两针一共转了720度。因为时针每分钟转过0.5度,分针每分钟转过6度,所以720÷(6+0.5)≈110.7分,约为l小时51分。
2、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子,剩余的空间为_____立方米。 B: 1500C: 5000D: 9000
参考答案: D 本题解释:【答案】D。解析:仓库的容量为250×10×4=10000立方米,1000个棱长为1米的正方体箱子体积为1000×1×1×1=1000立方米,则剩余空间为10000-1000=9000平方米,故正确答案为D。
3、在1至100这100个数中,有既不能被5整除也不能被9整除的数,它们的和是_____。
A: 1644B: 1779C: 3406D: 3541
参考答案: D 本题解释:【答案解析】先求出被5或9整除的数的和。1至100中被5整除的数有5,10,15,…,100,和为5+10+15+…+100=(100+5)×20÷2=10501至100中被9整除的数有9,18,…,99,和为9+18+27+…+99=(9+99)×11÷2=594又因为1~100中,45,90这两个数同时被5与9整除,于是所求的和是(1+2+…+100)-(5+10+…+100)-(9+18+…+99)+(45+90)=3541。因此,本题正确答案为D。
4、5个男生和3个女生排成一排,3个女生必须排在一起,有多少种不同排法?_____
A: 240B: 320C: 450D: 480
参考答案: B 本题解释: 答案【B】采用捆绑法,把3个女生视为一个元素,与5个男生进行排列,共有 A(6,6)=6x5x4x3x2种,然后3个女生内部再进行排列,有A(3,3)=6种,两次是分步完成的,应采用乘法,所以排法共有:A(6,6) ×A(3,3) =320(种)。
5、甲、乙两人从400米的环形跑道的一点A背向同时出发,8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米,那么,两人第三次相遇的地点与A点沿跑道上的最短距离是_____。
A: 166米 B: 176米 C: 224米 D: 234米
参考答案: B
6、现有红、黄、蓝三种颜色的珠子各若干颗,分给某班的52个学生,每个学生可以取1至3颗珠子,一种颜色的珠子最多只能取1颗。那么,这班学生中至少有_____人取的珠子完全相同。
A: 5B: 8C: 13D: 17
参考答案: B 本题解释:B[解析]取珠子的种类有如下7种:①红;②黄;③蓝;④红与黄;⑤红与蓝;⑥黄与蓝;⑦红、黄、蓝。从最不巧的情况想。每七个学生取的珠子的种类各不相同,因为52÷7(余3),所以,至少有7+1(即8)个人取的珠子完全相同。故本题正确答案为B。
7、甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要6小时,乙车单独清扫需要9小时,两车同时从东、西城相向开出,相遇时甲车比乙车多清扫15千米。问东、西两城城相距多少千米?_____
A: 60B: 75C: 90D: 135
参考答案: B 本题解释: 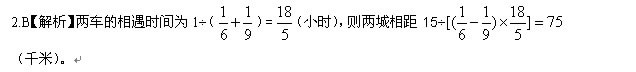
8、在一只底面半径是20cm的圆柱形小桶里,有一半径为l0cm的圆柱形钢材浸没在水中,当钢材从桶中取出后,桶里的水下降了3cm。求这段钢材的长度。_____
A: 3cmB: 6cmC: 12cmD: 18cm
参考答案: C 本题解释:【答案】C。解析:钢材的体积与水下降的体积相等,钢材长度与水下降的高度之比等于二者底面积之比的倒数,由此可得钢材长度为3×4=12。
9、小明和姐姐用2013年的台历做游戏,他们将12个月每一天的日历一一揭下,背面朝上放在一个盒子里,姐姐让小明一次性帮她柚出一张任意月份的30号或者31号。问小明一次至少应抽出多少张日历,才能保证满足姐姐的要求?_____
A: 346 B: 347 C: 348 D: 349
参考答案: C 本题解释:【答案】C。
10、1~100各数所有不能被9整除的自然数的和是_____。
A: 217B: 594C: 5050D: 4456
参考答案: D 本题解释:D解析:在1至100中,被9整除的数的和是9+18+27+…+99=9×(1+2+3+…+11)=9×66=5941至100各数之和是1+2+3+…+100=100(1+100)2=5050所以在1至100的各数中,所有不能被9整除的数的和是5050-594=4456。因此,本题正确答案为D。
11、从1、2、3、4中任取3个数组成没有重复的三位数的偶数的取法种数为_____。
A: 10 B: 12 C: 13 D: 11
参考答案: B 本题解释:【解析】B。 题干要求组成没有重复数字的三位数的偶数,所以只有尾数是2或4两种情况。当尾数是2时,有2×3=6(种);当尾数是4时,有2×3=6(种),所以共有6+6=12(种),故本题答案为B。
12、一次数学考试共有20道题,规定:答对一题得2分,答错一题扣1分,未答的题不计分。考试结束后,小明共得23分,他想知道自己做错了几道题,但只记得未答的题的数目是个偶数。请你帮助小明计算一下,他答错了多少道题_____
A: 3B: 4C: 5D: 6
参考答案: A 本题解释:【答案】A,代入即可,答对13道题,得26分,打错3道扣3分,未答的题的数目是4道恰好是个偶数。
13、王师傅在某个特殊岗位上工作,他每上8天班后,就连续休息2天。如果这个星期六和星期天他休息,那么,至少再过几个星期后他才能又在星期天休息?_____
A: 7个B: 10个C: 17个D: 70个
参考答案: A 本题解释:【解析】设至少过N个星期,可能第N个星期六与星期日连续休息,也可能第N个星期天与星期一连休2天,前者得出:7N-2=10K+8………………(1)后者得出7N-1=10K+8………………(2)其中K是自然数,由(1)得7N=10(K+1),因此,7N是10的倍数,N最小为10。由(2)得7N=10K+9,表明7N的个位数字是9,所以N=7,17,…。可见,至少再过7个星期后,才能又在星期天休息。故本题正确答案为A。
14、一个小数去掉小数部分后得到一个整数,这个整数加上原来的小数与4的乘积,得27.6。原来这个小数是_____。
A: 2.60B: 5.65C: 7.60D: 12.65
参考答案: B 本题解释:将原来的小数分成整数部分、小数部分和整个小数。此题可理解为:原小数的4倍与它的整数部分之和为27.6,这样27.6等于5个整数部分与4个小数部分之和。因为4个小数部分之和小于4,可知原小数的整数部分应满足:5倍整数<27<5倍整数+4,所以此整数为5。所以此小数为:5+(27.6-5×5)÷4=5.65,因此,本题正确答案为B。
15、某公司要到外地去推销产品,产品成本为每件3000元。从公司到外地距离是400千米,运费为每件产品每运1千米收1.5元。如果在运输及销售过程中产品的损耗是10%,那么公司要想实现25%的利润率,零售价应是每件多少元? _____
A: 4800B: 5000C: 5600D: 6000
参考答案: B 本题解释:【答案】B。解析:以1件商品为例,成本为3000元,运费为1.5×400=600元,则成本为3000+600=3600元,要想实现25%的利润率,应收入3600×(1+25%)=4500元;由于损耗,实际的销售产品数量为1×(1-10%)=90%,所以实际零售价为每件4500÷90%=5000元。
16、A、B、C三件衬衫的总价格为520元,分别按9.5折,9折,8.75折出售,总价格为474元,A、B两件衬衫的价格比为5﹕4,A、B、C三件衬衫的价格分别是多少元?()
A: 250,200,70B: 200,160,160C: 150,120,250D: 100,80,340
参考答案: B 本题解释:设A,B,C三件衬衫的价格分别为 ,
, ,
, ,则可以列方程组:
,则可以列方程组: ,
,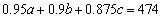 ,
, ,解得
,解得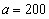 ,
, ,
, ,所以选B。
,所以选B。
17、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2,而4/9和151/301都大于1/2,所以只要比较二者的大小就可以,通过计算,151/301大,所以选择D。
18、某车间进行季度考核,整个车间平均分是85分,其中的人得80分以上(含80分),他们的平均分是90分,则低于80分的人的平均分是多少?_____
A: 68B: 70C: 75D: 78
参考答案: C 本题解释: 【解析】C。解法一、设x为所求,假设总共3人,其中2人80以上,1人低于80分。则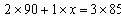 ,记住此处别忘了用尾数法快速得到答案;解法二、利用十字交叉法解决混合平均问题。两部分人比例为2︰1,则其各自平均分到85分的距离应该反过来为1︰2=5︰10,直接得到75。
,记住此处别忘了用尾数法快速得到答案;解法二、利用十字交叉法解决混合平均问题。两部分人比例为2︰1,则其各自平均分到85分的距离应该反过来为1︰2=5︰10,直接得到75。
19、有一块草地,上面的青草每天都生长得一样快。这块草地上的青草供20头牛吃,可以吃12天,或者供25头牛吃,可以吃8天。某人有牛70头,如果要保证青草不被吃完,需要在几块这样的草地上放牧?_____
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:【答案】A。解析:假设这块草地原有草量为x,每天长草量为y,每头牛每天吃草的量为1,则根据公式可得: 解得x=10,这块草地每天的长草量够10头牛吃。要保证青草不被吃完,需要在70÷10=7(块)这样的草地上放牧。
解得x=10,这块草地每天的长草量够10头牛吃。要保证青草不被吃完,需要在70÷10=7(块)这样的草地上放牧。
20、某班有35个学生,每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人,参加语文小组的有30人,参加数学小组的有13人。如果有5个学生三个小组全参加了,问有多少个学生只参加了一个小组?_____
A: 15人B: 16人C: 17人D: 18人
参考答案: A 本题解释:A【解析】利用三交集公式A+B+C=AUBUC+AnB+BnC+AnC-AnBnC(AnBnC是指语文,数学,英语三个都参加的人,AUBUC是只总人数),A+B+C=17+30+13,AnBnC=5,AUBUC=35,所求为AUBUC-(AnB+BnC+AnC)+AnBnC。 方便解法:参加一个小组的为x人,两个小组的为y人,x+y+5=35,x+2y+3×5=17+30+13,x=15。
21、某试卷共25题,答对的,一题得4分;答错或不答的,一题扣1分,小王得了60分,则小王答对了多少题?_____
A: 14B: 15C: 16D: 17
参考答案: D 本题解释: D [解析] 设答对了x道题,则未答对的题为(25-x)题,可得4x-(25-x)×1=60,解得x=17。故本题选D。
22、小明和小强从400米环形跑道的同一点出发,背向而行。当他们第一次相遇时,小明转身往回跑;再次相遇时,小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米,小强每秒跑5米,则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:A。两人相向运动,经过400÷(3+5)=50秒相遇,之后小明转身,两人做追及运动,经过400÷(5-2)=200秒第二次相遇;接着两人又做相向运动,经过50秒相遇,再做追及运动,经过200秒相遇,以此类推,第30次相遇共用30÷2×(50+200)=3750秒,则小明共跑了3×3750=11250米。
23、已知一杯茶水有若干克,第一次加入一定量的水后,茶水的浓度为6%,第二次又加入同样多的水后,茶水的浓度为4%,求第三次加入同样多的水后茶水的浓度为多少?_____
A: 1%B: 2%C: 3%D: 3.5%
参考答案: C 本题解释:C【解析】设第一次加完水后,含茶6份,含水94份,这样茶水浓度就为6%,第二次加完水后,茶水总量为6÷4%=150份,所以第二次加水为150-100=50份,第三次加入的水也为50份,茶水浓度为6÷(150+50)=0.03=3%。所以,第三次加入同样多的水后茶水的浓度变为3%。故本题正确答案为C。
24、现有200根相同的钢管,把它们堆放成正三角形垛,使剩余的钢管尽可能的少,那么乘余的钢管有_____。
A: 9B: 10C: 11D: 12
参考答案: B 本题解释:【解析】20层的情况是1-20的和,一共是210,超出了,所以减去最后一层20剩下190,所以剩余的钢管有200-190=10根。
25、如果两个四位数的差等于8921,那么就说这两个四位数组成一个数对,问这样的数对共有多少个?_____
A: 80B: 79C: 83D: 81
参考答案: B 本题解释:【解析】从两个极端来考虑这个问题:最大为9999-1078=8921,最小为9921-1000=8921,所以共有9999-9921+1=79个,或1078-1000+1=79个。故应选择B。
26、对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有_____。
A: 22人B: 28人C: 30人D: 36人
参考答案: A 本题解释:【答案解析】本题可以使用阴影覆盖法,即100-(40+18+20)=22(人),故远A项。
27、甲乙同时从A 地步行出发往B 地,甲60 米/分钟,乙90 米/分钟,乙到达B 地折返与甲相遇时,甲还需再走3 分钟才到达B 地,求AB 两地距离?_____
A: 1350B: 1080C: 900D: 750
参考答案: C 本题解释: 【解析】甲需要多走3分钟到B地,3×60=180米,速度比是2:3,所以路程比也是2:3,设全长X米,则(X-180)/(X+180)=2/3,求出X=900,实际也是选个180倍数的选项,排除AD。
28、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:C解析:汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+,1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶96(2/3)千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
29、一队战士排成三层空心方阵多出9人,如果在空心部分再增加一层,又差7人,问这队战士共有多少人?_____
A: 121B: 81C: 96D: 105
参考答案: D 本题解释:D[解一]由题意可得空心方阵再往里一层的总人数是:9+7=16(人),每边人数为:16÷4+1=5(人);所以3层空心方阵最外层每边人数为:5+2×3=11(人),总人数为:(11-3)×3×4=96(人);这队战士的总人数是:96+9=105(人)。[解二]相邻两层的人数之差为8人,最里层的人数为9+7+8=24人,次里层为24+8=32人,最外层为32+8=40人,所以总人数为24+32+40+9=105人。
30、一杯糖水,第一次加入一定量的水后,糖水的含糖百分比变为15%;第二次又加入同样多的水,糖水的含糖百分变比为12%;第三次再加入同样多的水,糖水的含糖百分比将变为多少?_____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:【答案】C。解析: 故正确答案为C。
故正确答案为C。
31、某单位有青年员工85人,其中68人会骑自行车,62人会游泳,既不会骑车又不会游泳的有12人,则既会骑车又会游泳的有_____人。
A: 57B: 73C: 130D: 69
参考答案: A 本题解释:【解析】68+62+12-85=57人。
32、某次抽奖活动在三个箱子中均放有红、黄、一绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少?_____
A: 在 0~25%之间B: 在25~50%之间C: 在50~75%之间D: 在75~100%之间
参考答案: C 本题解释:C。
33、某运输队有大货车和小货车24辆,其中小货车自身的重量和载货量相等,大货车的载货量是小货车的1.5倍,自身重量是小货车的2倍。所有车辆满载时共重234吨,空载则重124吨,那么该运输队的大货车有多少辆? _____
A: 4B: 5C: 6D: 7
参考答案: D 本题解释:D【解析】设大货车数量为x,小货车自重量为a,小货车数量为24-x,列方程x?2a+(24-x)?a=124[x?2a+(24-x)?a]+x?1 5a+(24-x)?a=234 解得x=7。故选D。
34、甲、乙、丙三人打羽毛球,每一局由两人上场,另一人做裁判。第一句抽签决定裁判,往后每一局的比赛在上一局的胜者和上一局的裁判之间进行。打了若干场之后,甲胜了10局,则乙和丙各负了8局,则他们至少打了_____局
A: 20B: 21C: 22D: 23
参考答案: C 本题解释:【答案】C。解析:根据题目,乙负了8局,说明乙做裁判至少8局,因此甲和丙打了8局,同理,丙负了8局,丙做裁判至少8局,说明甲和乙打了8局,因此甲,共打了8+8=16局,而甲胜了10局,说明甲输了6局,因此说明乙和丙打了6局,因此三人至少共打8+8+6=22局
35、甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。现在要把这四个旅行团分别进行分组,使每组都是A名游客,以便乘车前往参观游览。已知甲、乙、丙三个旅行团分成每组A人的若干组后,所剩的人数都相同,问丁旅行团分成每组A人的若干组后还剩几人?_____ B: 1C: 2D: 3
参考答案: B 本题解释:【解析】B。根据题意,知69、85、93对A同余。由85-69=16,93-85=8,93-69=24,可推出A=8或4或2,97÷8=12……1。所以丁团分成每组A人的若干组后还剩1人。
36、小张从家到单位有两条一样长的路.一条是平路、另一条是一半上坡路,一半下坡路,小张上班走这两条路所用的时间一样多。已知下坡的速度是平路的1.5倍,那么上坡的速度是平路的_____倍。
A: 3/5B: 2/5C: 1/4D: 3/4
参考答案: D 本题解释:【答案】D。解析:因为距离和时间都相同,则可以设路程是1,时间也是1,那么平路的速度为1÷1=1,又因为上坡和下坡路各一半也相同,那么上坡和下坡的路程都是O.5。下坡的速度为1.5,则下坡时问为0.5/1.5=1/3,因此上坡时间为1—1/3=2/3,上坡速度为1/2÷2/3=3/4。
37、某家店准备打折出售一批滞销的电脑,经核算,如果按正价打九折销售,每台还可盈利305元,如果打八折,就要亏损175元。那么这种电脑的进货价是_____元。
A: 4800B: 4625C: 4015D: 3940
参考答案: C 本题解释:这种电脑打九折和打八折的差价是305+175=480(元),那么正价为480÷(90%-80%)=4800(元),进货价为4800×90%-305=4015(元)。故本题答案为C。
38、某车间从3月2日开始每天调入人,已知每人每天生产~件产品,该车间从月1日至3月21日共生产840个产品.该车间应有多少名工人? _____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:【答案】B。解析:从3月2日开始调入的每一个人生产的产品的个数正好组成以1为公差的等差数列20,19,18,……1,得调入的人生产的总产品数是:(20+1)×20÷2=210(个),所以原有工人生产的产品数=840-210=630(个),每人每天生产一个,所以工人数=630/21=30(个)。
39、某年级有四个班级,不算一班有210人,不算二班有199人,不算三班有196人,不算四班有205人,问:这个年级共有_____人?
A: 240B: 270C: 320D: 3 60
参考答案: B 本题解释:B【解析】设一、二、三、四班的人数分别为a,b,c,d人。不算一班的人数是210人,即b+c+d=210;不算二班的人数是199人,即a+c+d=199;不算三班的人数是196人,即a+b+d=196;不算四班的人数为205人,即a+b+c=205;四个式子相加:3(a+k+c+d)=810。a+b+c+d=270,即这个年级共有270人,故应选B。
40、某医院内科病房有护士15人,每两人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次这两人再同值班,最长需要几天_____
A: 15B: 35C: 30D: 5
参考答案: B 本题解释:B.【解析】n×(n-1)/2=15×14/2=105,105×8/24=35。故选B。
41、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:【解析】:汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+,1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶96(2/3)千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
42、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月培训1290人次。问甲教室当月共举办了多少次这项培训? _____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:【解析】D。本题可直接看出答案,乙教室一次45人,共有1290人,所以乙次数一定为偶数,又因为一共27次,所以甲一定为奇数,直接选15。
43、两个运输队,第一队有320人,第二队有280人,现因任务变动,要求第二队的人数是第一队人数的2倍,需从第一队抽调多少人到第二队?_____
A: 80人B: 100人C: 120人D: 140人
参考答案: C 本题解释:C设需抽调x人,根据题意可得2(320-x)=280+x,解得x=120人。
44、甲、乙两种商品成本共2000元,商品甲按50%的利润定价,商品乙按40%的利润定价,后来打折销售,两种商品都按定价的80%出售,结果仍可得利润300元,甲种商品的成本是多少元?_____
A: 800 B: 700 C: 850 D: 750
参考答案: D 本题解释:【解析】D。 设甲种商品的成本为x元,则乙种商品的成本为2000-x元,可得:x×(1+50%)×80%+(2000-x)×(1+40%)×80%=2000+300,解得x=750。故选D项。
45、二十几个小朋友围成一圈,按顺时针方向一圈一圈地连续报数。如果报2和200的是同一个人,那么共有_____个小朋友。
A: 22B: 24C: 27D: 28
参考答案: A 本题解释:A【解析】小朋友的人数应是(200-2)=198的约数,而198=2×3×3×11。约数中只有2×11=22符合题意。
46、现有篮球、排球、乒乓球、足球、网球五门选修课,每名学生必须要从中选出而且仅选择2门选修课,问至少有多少名学生进行选课,才能保证至少有6名学生所选的选修课相同?_____
A: 48B: 50C: 51D: 70
参考答案: C 本题解释:【答案】C。解析:要求五门课程选出两门,共有C25=10种,要至少有6名学生所选的选修课相同,那么这10中选课方式各有5名学生选择,共有10×5=50人,之后再来一人,就可以保证有6名学生所选的选修课相同,则为50+1=51人,所以答案为C。
47、有一本畅销书,今年每册书的成本比去年增加了10%,因此每册书的利润下降了20%,但是今年的销量比去年增加了70%。则今年销售该畅销书的总利润比去年增加了_____。
A: 36%B: 25%C: 20%D: 15%
参考答案: A 本题解释:每本书的利润值下降了20%,为原来的0.8,销量增加了70%,为原来的1.7,1.7×0.8=1.36,1.36—1=0.36,即为36%。
48、三边长均为整数且最大边长为2009的三角形共有多少个?_____
A: 1008016 B: 1009020 C: 1010025 D: 2019045
参考答案: C 本题解释: C。根据三角形的构成原理,可知最大边长为2009时,另两边的和大于2009,差小于2009,则两边≤2009且≥1,则可知介于最长边与最短边之间的那条中边的长度必≥1005且≤2009。中边为1005时,另一边=1005,1种可能;中边为1006时,另一边=1004,1005,1006,共3种可能;中边为1007时,另一边=1003,1004,1005,1006,1007,共5种可能;……中边为2009时,另一边=1~2009,共2009种可能。因此三角形总和=1+3+5+…+2007+2009=1005(1+2009)/2=1010025种。所以答案为C项。
49、在同一环形跑道上小陈比小王跑得慢,两人都按同一方向跑步锻炼时,每隔12分钟相遇一次;若两人速度不变,其中一人按相反方向跑步,则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟?_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:不妨设小王和小陈速度分别为x,y,跑道长度为s,则:两人都按同一方向跑步锻炼时,每隔12分钟相遇一次,说明s/(x—y)=12;若两人速度不变,其中一人按相反方向跑步,则每隔4分钟相遇一次,说明s/(x+y)=4;解得s=6x=12y,所以两人跑完一圈花费的时间小陈比小王多6分钟。
50、甲、乙两人在一条环形跑道散步,两人从同一点A出发,背向而行。已知甲每分钟步行50米,乙每分钟步行30米,两人第一次在B点相遇,相遇后继续以原来的速度前进,第二次相遇在C点。若B、C两点沿环形跑道的较短距离为150米,则环形跑道的长度为多少米?_____
A: 400B: 450C: 560D: 600
参考答案: A 本题解释:【答案】A。解析:设环形跑道的长度为8x,甲、乙两人的速度比为5:3,则第一次相遇时,甲走的路程为5x、乙走的路程为3x;从第一次相遇到第二次相遇,甲的路程仍然是5x、乙的路程仍然是3x,可得3x=150,解得x=50。则环形跑道的长度为80×5=400(米)。因此,本题选择A选项。
51、从6名男生,5名女生中任选4人参加竞赛,要求男女至少各1名,有多少种不同的选法?_____
A: 240B: 310 C: 720 D: 1080
参考答案: B 本题解释: 答案【B】解析:此题从正面考虑的话情况比较多,如果采用间接法,男女至少各一人的反面就是分别只选男生或者女生,这样就可以变化成C(11,4)-C(6,4)-C(5,4)=310。
52、有4支队伍进行4项比赛,每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名,问总分最少的队伍最多得多少分? _____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:【答案】B 解析∶四项比赛的总得分是(5+3+2+1)×4=44分,A已得15分,最少得16分,剩下三人总得分最多为28分,要求得分最少的人得分最多且得分互不相同,则三人得分分别是8,9,11。此时一人得三项第二和一项第三,一人得一项第二和三项第三。
53、为帮助果农解决销路,某企业年底买了一批水果,平均发给每部门若干筐之后还多了12筐,如果再买进8筐则每个部门可分得10筐,则这批水果共有_____筐。
A: 192B: 198C: 200D: 212
参考答案: A 本题解释:【答案】A。解析:总数加8应能被10整除,如果为A,则部门数为20;如果为D,部门数为22,则212÷22=9……14不符合题意。故选择A。
54、出租车在7公里以内收费10.6元(不足7公里按7公里收费),以后每走1公里收费1.8元,某乘客有一次乘出租车花了34元,他乘坐了多少公里?_____
A: 16B: 17C: 20D: 23
参考答案: C 本题解释:C解析:设他乘坐了x公里,根据题意列方程,得:10.6+(x-7)×1.8=34,解得:x=20,选C。
55、学习委员收买练习本的钱,她只记下四组各交的钱,第一组2.61元,第二组3.19元,第三组2.61元.第四组3.48元,又知道每本练习本价格都超过1角,全班共有多少人?_____
A: 29B: 33C: 37D: 41
参考答案: D 本题解释:D。把所有的钱换算成以分为单位的即可。只需要找到261、319和348的超过10的公约数即可,容易得到,这三个数的最大公约数是29,满足题意,因此每本练习本的价格是29分,那么全班有41个人
56、某市出租车收费标准是:5千米内起步费10.8元,以后每增加1千米增收1.2元,不足1千米按1千米计费。现老方乘出租车从A地到B地共支出24元,如果从A地到B地先步行460米,然后再乘出租车也是24元,那么从AB的中点C到B地需车费_____元。(不计等候时间所需费用)
A: 12B: 13.2C: 14.4D: 15.6
参考答案: C 本题解释:经济M题。共花钱24元,超过5千米的部分为24-10.8=13.2(元),超过5千米后走了13.2÷1.2=11(千米),总路程最多为16千米,因为步行460米后花费相同,说明460米后的路程一定超过15千米,则总路程15+0.46<S≤16,则C到B的距离7.73<< p>S/2≤8,因不足1千米按1千米计费,故应看成8千米,共花费10.8-9(8-5)×1.2=14.40(元)。
57、用两根同样长度的铁丝分别圈成圆形和正方形,圆形面积大约是正方形面积的几倍?_____
A: 3π B: 4/π C: 5π D: 6π
参考答案: B 本题解释: 【解析】B。设铁丝长度为X,则围成圆形的半径为X/2π,故面积为X2/4π,而其围成的正方形边长为x/4,则其面积为X2/16,所以圆形面积为正方形面积的4/π倍。
58、建华中学共有1600名学生,其中喜欢乒乓球的有1180人,喜欢羽毛球的有1360人,喜欢篮球的有1250人,喜欢足球的有1040人,问以上四项球类运动都喜欢的至少有几人?_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析:采取逆向思维法。不喜欢乒乓的1600-1180=420,不喜欢羽毛球的1600-1360=240,不喜欢篮球的1600-1250=350,不喜欢足球的1600-1040=560,要使四项运动都喜欢的人数最少,那么不喜欢的人数就要最多那么都尽量不相交,从而达到最多:420+240+350+560=1570人,所以喜欢的最少的为1600-1570=30人,故正确答案为B。
59、六个盘子中各放有一块糖,每次从任选的两个盘子中各取一块放入另一个盘子中,这样至少要做多少次,才能把所有的糖都集中到一个盘子中_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:【答案】B。解析:开始时是1,1,1,1,1,1,第二次变为0,0,3,1,1,1,第三次变为2,0,2,0,1,1,第三次变为4,0,1,0,0,1,第四次变为6,0,0,0,0,0。
60、已知一个长方体的长、宽、高分别为10分米、8分米和6分米,先从它上面切下一个最大的正方体,然后再从剩下的部分上切下一个最大的正方体。问切除这两个正方体后,最后剩下部分的体积是多少?_____
A: 212立方分米B: 200立方分米C: 194立方分米D: 186立方分米
参考答案: B 本题解释:【答案解析】根据题意可知,第一次切下的正方体的边长为6分米,第二次切下的正方体的边长为4分米,故最后剩下部分的体积是10×8×6-6×6×6-4×4×4=200立方分米。
61、五个瓶子都贴有标签,其中恰好贴错了三个,贴错的可能情况有多少种?_____
A: 60B: 46C: 40D: 20
参考答案: D 本题解释:D【解析】根据题意贴错三个,贴对两个。首先从五个瓶子中选出3个的种类为C35=10种,这三个瓶子为贴错标签的,这三个瓶子贴错标签的有两种情况。所以五个瓶子中贴错三个标签的情况有10×2=20种。
62、在9×9的方格表中,每行每列都有小方格被染成黑色,且一共只有29个小方格为黑色。如果a表示至少包含5个黑色小方格的行的数目,b表示至少包含5个黑色小方格的列的数目,则a+b的最大值是_____。
A: 25B: 10C: 6D: 14
参考答案: B 本题解释:B【解析】假设a+b≥11,且a≥b,则2a≥11,因为不存在染半格的情况,所以a≥6。那么这a行中至少有黑色小方格6×5=30(个),与题干中只有29个黑色小方格的条件相矛盾,因此假设不成立,a+b≤10,当a+b=10时,黑色小方格的分布如下图。故本题答案为B。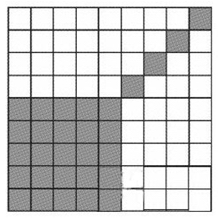
63、某计算机厂要在规定的时间内生产一批计算机,如果每天生产140台,可以提前3天完成;如果每天生产120台,就要再生产3天才能完成。问规定完成的时间是多少天?_____
A: 30B: 33C: 36D: 39
参考答案: D 本题解释:答案:D【解析】解答此题可以同时使用代入法和方程法。为快速解题可首先考虑方程法,设规定时间为x天,则(x-3)×l40=(x+3)×l20,解得x=39。故选D。
64、小刚买了3支钢笔,1个笔记本,2瓶墨水花去35元钱,小强在同一家店买同样的5支钢笔,1个笔记本,3瓶墨水花去52元钱,则买1支钢笔,1个笔记本,1瓶墨水共需_____元。
A: 9B: 12C: 15D: 18
参考答案: D 本题解释:【答案】D。解析:解法一:设钢笔价格为X元,笔记本价格为Y元,墨水价格为Z元,可得方程组:3X+Y+2Z=35…①5X+Y+3Z=52…②×2-②:X+Y+Z=18元解法二:设钢笔价格为0,笔记本价格为X元,墨水价格为Y元,可得方程组:X+2Y=35…①X+3Y=52…②解得Y=17,X=1所以三者价格之和为0+1+17=18元。因此本题正确答案为D。
65、有甲、乙两只钟表,甲表8时15分时,乙表8时31分。甲表比标准时间每9小时快3分,乙表比标准时间每7小时慢5分。至少要经过几小时,两钟表的指针指在同一时刻?_____
A: 12(7/11)B: 15C: 15(3/11)D: 17(8/11)
参考答案: C 本题解释: C 解析: 甲表比标准时间每小时快3/9=1/3分,乙表比标准时间每小时慢5/7分。甲、乙两表每小时相差是1/3+5/7=22/21分8时31分-8时15分=16分按追及问题,追及路程为16分,速度差是每小时22/21分,求追及时间。16÷22/21=16×21/22=15(3/11)(小时)至少再经过15311小时,两钟表的指针指在同一时刻。
66、食堂购进200斤含水量为90%的西红柿,3天后再测试发现西红柿的含水量变为80%,那么这批西红柿的总重量共减少了_____千克。
A: 100B: 10C: 20D: 50
参考答案: D 本题解释:D【解析】西红柿的水分蒸发,但水分之外的其他物质的重量并没有改变,由此可知现在西红柿的重量为:200×(1-90%)÷(1-80%)=100(斤)。那么这批西红柿的重量共减少了200-100=100(斤)=50(千克)。故本题答案为D。
67、商场销售某种商品的加价幅度为其进货价的40%,现商场决定将加价幅度降低一半来促销,商品售价比以前降低了54元。问该商品原来的售价是多少元?_____
A: 324B: 270C: 135D: 378
参考答案: D 本题解释:假设进价是10份,则原来售价是14份,现在售价是12份。差2份是54元,那么14份是54×7=378(元)。
68、某国家对居民收入实行下列税率方案;每人每月不超过3000美元的部分按照1%税率征收,超过3000美元不超过6000美元的部分按照X%税率征收,超过6000美元的部分按Y%税率征收(X,Y为整数)。假设该国某居民月收入为6500美元,支付了120美元所得税,则Y为多少_____
A: 6B: 3C: 5D: 4
参考答案: A 本题解释:A【解析】该国某居民月收入为6500美元要交的所得税为3000×1%+3000×X%+(6500-3000-3000)×Y%=120,化简为6X+Y=18,由于6X和18都能被6整除,因此Y也一定能被6整除分析选项,只有A符合。
69、设有9个硬币,其中有1分、5分、1角以及5角四种,且每种硬币至少有1个。若这9个硬币总值是1.77元,则5分硬币必须有几个?_____
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:C。【解析】由题意知,每种硬币至少有1个,则知四种硬币各1个共0.66元,又由于硬币总值为1.77元,则还需增加1.11元,即5个硬币,从而需硬币1分1个,硬币5角2个,最后还需有1角。由于题意表明有9个硬币,应选2个5分硬币,因而共有3个5分硬币。
70、A大学的小李和B大学的小孙分别从自己学校同时出发,不断往返于A、B两校之间。现已知小李的速度为85米/分,小孙的速度为105米/分,且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时,两人合起来走过的距离恰为A、B两校距离的3倍,因此A、B两校相距(85+105)×12÷3=760(米)。故选D。
71、173×173×173-162×162×162=_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:答案:D【解析】利用简单的猜测法。173的尾数是3,3的立方为27;162的尾数是2,2立方为8。两者相减尾数为9,所以判断173和162的立方之差的尾数为9。所以答案为D项。
72、如果某商店 以每打1.8元的价格购进6打小工艺品(每打12件).之后又以每件0.2元卖出.这些小商品全部卖完后商店可得多少利润?_____
A: 32元 B: 3.6元 C: 2.4元 D: 2.84元
参考答案: B 本题解释:B【解析】0.2×12×6-1.8×6=3.6,一打=12个。
73、一件工作甲先做6小时,乙接着做12小时可以完成。甲先做8小时,乙接着做6小时也可以完成。如果甲先做3小时后,再由乙接着做,还需要多少小时完成? _____
A: 16B: 18C: 21D: 24
参考答案: C 本题解释:C【解析】设甲、乙两人每小时的工作量x、y,可列方程6x+12y=18x+6y=1 解得x=110y=130,甲先做了110×3,工作还剩1-310=710,故乙还需要710÷130=21 小时。故选C。
74、有一个电子钟,每走8分钟亮一次灯,每到整点响一次铃。中午12点整,电子钟响铃又亮灯。下一次既响铃又亮灯是几点钟?_____
A: 1B: 2C: 3D: 4
参考答案: B 本题解释:【答案】B。解析:8分钟和一个小时(60分钟)的最小公倍数是120分钟,所以再过120分钟又一次既响铃又亮灯。
75、50名同学面向老师站成一行。老师先让大家从左至右按1,2,3,…依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。问:现在面向老师的同学还有多少名?_____
A: 30B: 34C: 36D: 38
参考答案: D 本题解释: D【解析】 第一次报4的倍数的12名同学向后转后,在报6的倍数的8名同学中,面向老师和背向老师的各4名。分析如下:报4的倍数的同学分别报4,8,12,16,20,24,28,…,48;报6的倍数的同学分别报6,12,18,24,30,…,48;第二次报6的倍数的同学中有4名同学的报数与第一次报4的倍数的同学相同,故两次报数结束后,先前4名背向老师的同学又面向老师,另外4名同学则背向老师。故可推出,背向老师的同学有12名,面向老师的同学有38名。因此,本题正确答案为D。
76、校对一份书稿,编辑甲每天的工作效率等于编辑乙、丙每天工作效率之和,丙的工作效率相当于甲、乙每天工作效率之和的1/5。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿,则需要_____天才能完成。
A: 20B: 16C: 24D: 18
参考答案: D 本题解释:D 解析:三人一起完成校对需要6天,那么三人每天的效率之和是1/6。因为甲每天的工作效率等于乙、丙每天工作效率之和,那么甲的工作效率为1/12,乙、丙的效率和也是1/12。设乙单独完成校对需要x天,那么根据题意可得到方程:1/12-1/x=(1/12+1/x)×1/5解得x=18,即乙单独完成校对需要18天,正确答案为D。
77、某国家对居民收入实行下列税率方案;每人每月不超过3000美元的部分按照1%税率征收,超过3000美元不超过6000美元的部分按照X%税率征收,超过6000美元的部分按Y%税率征收(X,Y为整数)。假设该国某居民月收入为6500美元,支付了120美元所得税,则Y为多少_____
A: 6B: 3C: 5D: 4
参考答案: A 本题解释:答案: A 解析:该国某居民月收入为6500美元要交的所得税为3000×1%+3000×X%+(6500-3000-3000)×Y%=120,化简为6X+Y=18,由于6X和18都能被6整除,因此Y也一定能被6整除分析选项,只有A符合。
78、小张、小王二人同时从甲地出发,驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快,两人出发后第一次和第二次相遇都在同一地点,那么小张的车速是小王的_____倍。
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:【解析】B。行程问题。采用比例法。由题意,两人从同地出发,则第一次相遇时两人的路程和为2个全程,设其中小张走了x,小王走了y;第二次相遇 时两人走了4个全长,小张走了2y,小王走了x-y;由比例法x÷y=2y÷(x-y),解得x=2y,故两人速度比为2:1。
79、甲、乙、丙三人沿着400米环形跑道进行800米跑比赛,当甲跑1圈时,乙比甲多跑17圈,丙比甲少跑17圈。如果他们各自跑步的速度始终不变,那么,当乙到达终点时,甲在丙前面_____。
A: 85米 B: 90米C: 100米 D: 105米
参考答案: C 本题解释:【解析】C。甲跑 1 圈,乙比甲多跑 17 圈,即 87 圈,丙比甲少跑 17 圈,即 67 圈,则甲、乙、丙三人速度之比为 7 ∶ 8 ∶ 6 。所以,当乙跑完 800 米 时,甲跑了 700 米 ,丙跑了 600 米 ,甲比丙多跑了 100 米 。
80、下列哪项能被11整除? _____
A: 937845678B: 235789453C: 436728839D: 867392267
参考答案: A 本题解释:A【解析】9+7+4+6+8=343+8+5+7=2334-23=11所以,答案是A。
81、某旅游景点商场销售可乐,每买3瓶可凭空瓶获赠1瓶可口可乐,某旅游团购买19瓶,结果每人都喝到了一瓶可乐,该旅游团有多少人?_____
A: 19B: 24C: 27D: 28
参考答案: D 本题解释: D 解析:由题意知:买2瓶可乐就可以喝3瓶,所以19:N=2:3,N=28.5,商家不可能亏本,所以取28,选D。
82、某班有50位同学参加期末考试,结果英文不及格的有15人,数学不及格的有19人,英文和数学都及格的有21人。那么英文和数学都不及格的有_____人。
A: 4B: 5C: 13D: 17
参考答案: B 本题解释:本题正确答案为B。解析:设英文和数学都不及格的有x人,由容斥原理可得15+19-x=50-21,得x=5,故选B。
83、小王和小李6小时共打印了900页文件,小王比小李快50%。请问小王每小时打印多少页文件?_____
A: 60B: 70C: 80D: 90
参考答案: D 本题解释: 【解析】D。设小王每小时打印X页,因为小王比小李快50%,则小李每小时打印为X (1-50%)页,则根据题意可列:6X (1-50%)+6X=900,则X=90。
84、小张每连续工作5天后休息3天,小周每连续工作7天后休息5天。假如3月1日两人都休息,3月2日两人都上班,问三月份有多少天两人都得上班?_____
A: 12B: 14C: 16D: 18
参考答案: B 本题解释:【答案】B。解析:解析1:前者8天一个循环周期,后者12天一个循环周期,两者最小公倍数为24。在三月份中从3月2日到3月25日,两人重合的工作天数为9天。在3月26日至3月31日的6天中,前5天两人同时工作。因此共计14天。故正确答案为B。解析2:用图表示如下,其中×表示工作,○表示休息,下图从3月2日起:小张:×××××○○○×××××○○○×××××○○○×××××○小周:×××××××○○○○○×××××××○○○○○××××××由图可知有14天两人都得上班。故正确答案为B。
85、共计33个三角形和四边形,有111个角,则四边形的个数为_____。
A: 10B: 11C: 12D: 13
参考答案: C 本题解释: C [解析] 设四边形的个数为x,由题意可得:4x+(33-x)×3=111,解得x=12,即应该有12个四边形。故本题选C。
86、某单位职工24人中,有女性11人,已婚的有16人。已婚的16人中有女性6人。问这个单位的未婚男性有多少人?_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: B 解析:由题意:未婚共有:24-16=8人,其中未婚女性有:11-6=5人,故未婚男性有:8-5=3人,选B。
87、四个学生做加法练习,任写一个六位数,然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数,最后把这个新六位数与原数相加,分别得到以下四个六位数。则哪个结果有可能正确? _____
A: 172536B: 568741C: 620708D: 845267
参考答案: C 本题解释: 
88、某技校安排本届所有毕业生分别去甲、乙、丙3个不同的工厂实习。去甲厂实习的毕业生占毕业生总数的32%,去乙厂实习的毕业生比甲厂少6人,且占毕业生总数的24%.问去丙厂实习的人数比去甲厂实习的人数_____。
A: 少9人B: 多9人C: 少6人D: 多6人
参考答案: B 本题解释:【答案】B。解析:根据题意去甲厂实习的人数占32%,去乙厂实习的人数占24%,因此去丙厂实习的人数占1-32%-24%=44%,故去丙厂的人数比去甲厂多44%-32%=12%;而去甲厂实习的人数比去乙厂的多32%-24%=8%,为6人,故去丙厂的人数比去甲厂的应多6÷8%×12%=9人,故答案选B。
89、出租车在开始10千米以内收费10.5元,以后每走1千米,收费1.7元。请问走25千米需收多少钱?_____
A: 20.6元 B: 35元 C: 36.5元D: 36元
参考答案: D 本题解释:D
90、在一条长100米的道路上安装路灯,路灯的光照直径是10米,请问至少要安装多少盏灯?_____
A: 11 B: 9 C: 12 D: 10
参考答案: D 本题解释:D【解析】最少的情况发生在,路灯的光形成的圆刚好相切。要路灯的光照直径是10米,即灯照的半径为5米,因此第一个路灯是在路的开端5米处,第二个在离开端15米处,第三个在25米处……第十个在95米处,即至少要10盏。
91、甲、乙、丙三名运动员囊括了全部比赛项目的前三名,他们的总分分别是8、7和17分,甲得了一个第一名,已知各个比赛项目分数相同,且第一名的得分不低于二、三名得分的和,那么比赛共有多少个项目?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分,每个项目前三名的分数和至少是3+2+1=6分,所以每个项目前三名的分数和应该是32的大于6的约数,只能是8、16、32;如果是16或32,因为甲得了一个第一,所以甲的得分应大于8,不合题意,所以每个项目前三名的分数和是8分,共有项目32÷8=4个。
92、5人的体重之和是423斤,他们的体重都是整数,并且各不相同,则体重最轻的人最重可能重_____
A: 80斤 B: 82斤 C: 84斤 D: 86斤
参考答案: B 本题解释:B。【解析】5个80斤的则为400斤,剩余23斤,分一下。 从0、1、2、3、4、5、6、7中选,最轻只有选2了,如选3,则3、4、5、6、7加起来超过23。所以为82斤。
93、甲、乙两校共有毕业生180人,两校各买了一批纪念册,给本校毕业生每人一本后,甲校余116本,乙校余114本。经研究两校各向彼校毕业生每人送一本纪念册,送后甲校还比乙校多剩10本。问甲校的毕业生人数比乙校的毕业生人数多多少人?_____
A: 20人B: 16人C: 10人D: 8人
参考答案: D 本题解释:【解析】解一:由题意知,两校各给本校毕业生每人一本后共余下116+114=230本。两校再各向彼校毕业生每人送一本后共余下230-180=50本,而这时甲校比乙校多余下10本,故知此时甲校还余下(50+10)÷2=30本,乙校还余下(50-10)÷2=20本。而两校各给对方每个毕业生送了一本后,相当于两校买的纪念册各发了180本,所以甲校买了30+180=210本,乙校买了20+180=200本,甲、乙两校的毕业生人数分别是210-116=94人,200-114=86人。二者之差94-86=8人。故选D。解二:第一次分发毕业纪念册后,甲校余下的比乙校多116-114=2本,给彼校分发完毕后,甲校比乙校剩余的多10本,由此可推断甲校学生比乙校多10-2=8人,故选D。
94、一个盒子里面装有10张奖券,只有三张奖券上有中奖标志,现在5人每人摸出一张奖券,至少有一人的中奖概率是多少? _____
A: 4/5 B: 7/10 C: 8/9 D: 11/12
参考答案: D 本题解释:D【解析】至少有一人中奖,那算反面就是没有人中1-(7/10)×(6/9) ×(5/8) ×(4/7) ×(3/6)=11/12。
95、用1,2,3,4,5这五个数字组成没有重复数字的自然数,从小到大顺序排列:1,2,3,4,5,12,……,54321。其中,第206个数是_____
A: 313 B: 12345 C: 325 D: 371
参考答案: B 本题解释:B。由1、2、3、4、5组成的没有重复数字的一位数共有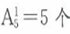 ;二位数共有个
;二位数共有个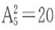 ;三位数共有个
;三位数共有个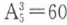 ;四位数共有个
;四位数共有个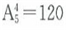 ;至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个;那么第206个数是第一个由1、2、3、4、5组成的五位数,即最小的五位数12345。
;至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个;那么第206个数是第一个由1、2、3、4、5组成的五位数,即最小的五位数12345。
96、有两只相同的大桶和一只空杯子,甲桶装牛奶,乙桶装糖水,先从甲桶内取出一杯牛奶倒入乙桶,再从乙桶取出一杯糖水和牛奶的混合液倒人甲桶,请问,此时甲桶内的糖水多还是乙桶内的牛奶多?_____。
A: 无法判定B: 甲桶糖水多C: 乙桶牛奶多D: 一样多
参考答案: D 本题解释:D【精析】假设乙桶内有N杯糖水,从甲中取出1杯牛奶倒入乙桶,乙桶中有l杯牛奶和N杯糖水。均匀后,再从乙桶取出一杯糖水和牛奶的混合物倒入甲桶,这杯混合物中有牛奶1/N+1杯有糖水N/N+1杯,因此乙桶中剩余的牛奶有N/N+1杯,而倒入甲桶中的糖水也有而N/N+1杯。甲桶内的糖水和乙桶内的牛奶一样多。
97、用 直线切割一个有限平面,后一条直线与此前每条直线都要产生新的交点。第1条直线将平面分成2块,第2条直线将平面分成4块,第3条直线将平面分成7块,按此规律将该平面分为22块需:_____
A: 5条直线B: 6条直线C: 7条直线D: 8条直线
参考答案: A 本题解释:增加的面的个数:交第一条直线,分割两个面,以后交一条直线,则增加的面的个数为交点增加数加1,即(n-1+1) = n 故对n条直线,面数为 n + (n-1) + …… + 2 + 2 = n(n+1)/2 +1 注意:开始面上只有1条直线时已有2个面,故最小为2。总结下:对第n条直线: 面数:n(n+1)/2 +1 故答案为6。
98、假设7个相异正整数的平均数是14,中位数是18,则次7个正整数中最大数是多少?_____
A: 58B: 44C: 35D: 26
参考答案: C 本题解释:【答案】C。解析:构造数列问题。此题告诉我们平均数是14,则总和为14*7=98,中位数为18,总共7个数,意味着小于18的有3个数,大于18的有3个数,为了保证最大的数大,所以我们要让大于18的数尽可能的小,则其他的两个数我们可以定义为19,20;所以得到的式子为18+19+20+n<98,所以n<41,则小于41的最大选项为35,所以选择C选项。
99、一个班有50名学生,他们的名字都是由2个或3个字组成的。将他们平均分为两组之后,两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5B: 8C: 10D: 12
参考答案: C 本题解释:【解析】C。不定方程问题。由题意两组学生名字字数相差10,两边人数相同,即其中一组比另一组三名字人数多10人,则2名字人数少10人。
100、毛毛骑在牛背上过河,他共有甲、乙、丙、丁4头牛,甲过河要2分钟,乙过河要3分钟,丙过河要4分钟,丁过河要5分钟。毛毛每次只能赶2头牛过河,要把4头牛都赶到对岸去,最少要多少分钟? _____
A: 16B: 17C: 18D: 19
参考答案: A 本题解释:A。若要时间最短,则一定要让耗时最长的两头牛同时过河。先骑甲、乙过河,骑甲返回,共用5分钟;再骑丙、丁过河,骑乙返回,共用8分钟;最后再骑甲、乙过河,用3分钟,共用时5+8+3=16分钟。