时间:2016-06-07 06:58:23
1、三条边均为正整数,且最长边为11的三角形有_____个。
A: 21B: 23C: 25D: 36
参考答案: D 本题解释:参考答案 题目详解:分情况考虑:根据“三角形两边之和大于第三边”:最短边为1,那么另一边为11,一种;最短边2,另一边可以是11、10,二种;最短边为3,另一边可以是9、10、11,三种;……最短边6,另一边可以是6、7、8、9、10、11,六种;最短边7,另一边可以是7、8、9、10、11,五种;最短边8,另一边可以是8、9、10、11,四种;……最短边11,另一边只能是11,一种;计算总共有几种情况:
题目详解:分情况考虑:根据“三角形两边之和大于第三边”:最短边为1,那么另一边为11,一种;最短边2,另一边可以是11、10,二种;最短边为3,另一边可以是9、10、11,三种;……最短边6,另一边可以是6、7、8、9、10、11,六种;最短边7,另一边可以是7、8、9、10、11,五种;最短边8,另一边可以是8、9、10、11,四种;……最短边11,另一边只能是11,一种;计算总共有几种情况: 种。所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
种。所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
2、一个正方形的一边减少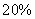 ,另一边增加2,得到长方形的面积与原正方形的面积相等,问正方形面积是多少?_____
,另一边增加2,得到长方形的面积与原正方形的面积相等,问正方形面积是多少?_____
A: 8B: 10C: 16D: 64
参考答案: D 本题解释:参考答案 题目详解:设原来正方形的边长为
题目详解:设原来正方形的边长为 米:
米: 所以原来正方形的边长为8米;所以原来正方形的面积:
所以原来正方形的边长为8米;所以原来正方形的面积: ;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
3、依次连接正方形各边的中点得到新的正方形,如此反复三次。如图,阴影部分与空白部分的面积之比是_____。 
A: 3:1B: 3:2C: 5:3D: 5:2
参考答案: C 本题解释:参考答案:C题目详解:根据几何知识点:注意连正方形的各边中点所形成正方形的面积是原正方形的 ;空白各个部分的的面积:中间空白正方形是大正方形面积的
;空白各个部分的的面积:中间空白正方形是大正方形面积的 ;中间四块空白三角形面积之和是大正方形面积的
;中间四块空白三角形面积之和是大正方形面积的 ;空白总面积:空白面积占总面积的
;空白总面积:空白面积占总面积的 ;所以阴影部分与空白部分的面积之比是:
;所以阴影部分与空白部分的面积之比是: ;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
4、在太阳光照射下,一个高为3米的竹杆其影子长为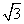 米,则一个半径为1米的球其影子最长为:
米,则一个半径为1米的球其影子最长为: 
A: 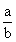 B:
B: 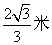 C:
C: 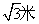 D:
D: 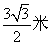
参考答案: 本题解释:参考答案:C题目详解:根据题意:AB是竹竿的长度为3米,BC是影子的长度为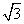 米;由tanA=a/b可以计算光线与影子形成的角度∠ACB:由tan∠ACB=a/b,a=AB=3;b=BC=
米;由tanA=a/b可以计算光线与影子形成的角度∠ACB:由tan∠ACB=a/b,a=AB=3;b=BC=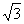 得,tan∠ACB=a/b=
得,tan∠ACB=a/b=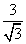 =
=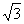 ,则∠ACB=60°半径为1米的球体形成的影子的最远点是光线与球体相切点处形成的影子;假设光线与半径为1米的球体相切于E点,则F点是球体形成影子的最远点,即DF为球体形成的影子。作CM⊥EF于M:则有:CM=OE=1。在直角三角形△CFM里:∠CFM=∠ACB=60°。由sinA=a/c,a=CM=1,∠A=∠CFM=60°;得CF=c=a/sinA=1/sin60°=1÷
,则∠ACB=60°半径为1米的球体形成的影子的最远点是光线与球体相切点处形成的影子;假设光线与半径为1米的球体相切于E点,则F点是球体形成影子的最远点,即DF为球体形成的影子。作CM⊥EF于M:则有:CM=OE=1。在直角三角形△CFM里:∠CFM=∠ACB=60°。由sinA=a/c,a=CM=1,∠A=∠CFM=60°;得CF=c=a/sinA=1/sin60°=1÷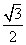 =
=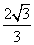 ;在直角三角形△OCD里:∠OCD=∠ACB=60°。由tanA=a/b,a=OD=1,∠A=∠OCD=60°得,DC=b=a/tanA=1/tan60°=1÷
;在直角三角形△OCD里:∠OCD=∠ACB=60°。由tanA=a/b,a=OD=1,∠A=∠OCD=60°得,DC=b=a/tanA=1/tan60°=1÷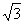 =
=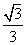 ,DF=DC+CF=
,DF=DC+CF=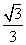 +
+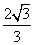 =
=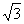 ;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
5、右图是由5个相同的小长方形拼成的大长方形,大长方形的周长是88厘米,问大长方形的面积多少平方厘米?_____ 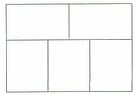
A: 472平方厘米B: 476平方厘米C: 480平方厘米D: 484平方厘米
参考答案: C 本题解释:参考答案:C题目详解:观察大长方形的上下两边,可知:小长方形的长宽比为3:2;设小长方形长宽分别为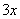 、
、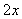 :则周长
:则周长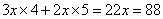 ,
,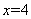 ,即大长方形的长为:
,即大长方形的长为: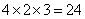 ;宽为:
;宽为: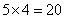 大长方形的面积为:
大长方形的面积为: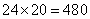 (平方厘米);所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
(平方厘米);所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
6、(2008安徽)用两根同样长度的铁丝分别圈成圆形和正方形,圆形面积大约是正方形面积的几倍?_____
A: 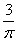 B:
B: 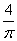 C:
C: 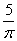 D:
D: 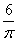
参考答案: B 本题解释:参考答案:B题目详解:依题意:假设圆的半径为 ,正方形的边长为
,正方形的边长为 ;由于周长相同(同样长度的铁丝):
;由于周长相同(同样长度的铁丝): 。其面积比应该为:
。其面积比应该为: ;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
7、半径为5厘米的三个圆弧围成如右图所示的区域,其中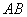 弧与
弧与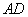 弧为四分之一圆弧,而
弧为四分之一圆弧,而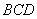 弧是一个半圆弧,则此区域的面积是多少平方厘米?_____
弧是一个半圆弧,则此区域的面积是多少平方厘米?_____ 
A: 25B: 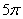 C.50D:
C.50D: 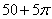
参考答案: C 本题解释:参考答案:C题目详解:根据图形:过B,D点分别做垂线;过A点做BD的平行线,连接各点;为一长方形;等于所求图形面积;长方形面积等于: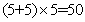 ;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
8、一个长方形的周长是130厘米,如果它的宽增加 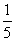 ,长减少
,长减少 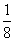 ,就得到一个相同周长的新长方形。原长方形的面积是多少?_____
,就得到一个相同周长的新长方形。原长方形的面积是多少?_____
A: 250平方厘米B: 400平方厘米C: 10000平方厘米D: 1000平方厘米
参考答案: D 本题解释:参考答案 题目详解:依题意可知:长的
题目详解:依题意可知:长的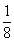 和宽的
和宽的 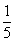 相等即长和宽的比是
相等即长和宽的比是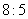 ;长方形的长、宽为:长=
;长方形的长、宽为:长=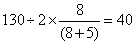 厘米;宽=
厘米;宽=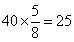 厘米;原长方形的面积:
厘米;原长方形的面积: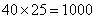 平方厘米。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
平方厘米。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
9、(2008江苏)台风中心从A地以每小时20公里的速度向东北方向移动,离台风中心30公里内的地区为危险区,城市B在A的正东40公里处。B城位于危险区的时间为_____。
A: ,B两村庄分别在一条公路L的两侧,A到L的距离|AC|为1公里,B到L的距离|BD|为2公里,C,D两处相距6公里,欲在公路某处建一个垃圾站,使得A,B两个村庄到此处处理垃圾都比较方便,应建在离C处多少公里?(C)B: 1小时C: 0.5小时D: 2小时
参考答案: B 本题解释:参考答案:B题目详解: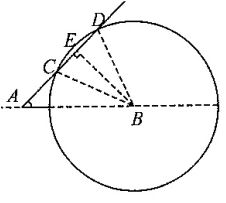 根据题目,可知:以城市B为圆心,30公里为半径画圆,与台风的轨迹交于C、D两点,其内部即为危险区。台风从C点移动到D点的时间是城市B受影响的时间;由题可知:∠BAD=45°;AB=40;在直角三角形△ABE里,设
根据题目,可知:以城市B为圆心,30公里为半径画圆,与台风的轨迹交于C、D两点,其内部即为危险区。台风从C点移动到D点的时间是城市B受影响的时间;由题可知:∠BAD=45°;AB=40;在直角三角形△ABE里,设 根据sinA=
根据sinA=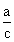 ,AB=40,∠A=45°;得:BE=a=c×sinA=40×sin45°=40×
,AB=40,∠A=45°;得:BE=a=c×sinA=40×sin45°=40×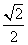 =
=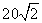 。在直角三角形△ABE里,根据勾股定理得:
。在直角三角形△ABE里,根据勾股定理得: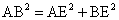 ,即
,即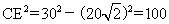 ;则:CE=
;则:CE=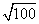 =10,CD=2×CE=2×10=20;B城处于危险区内的时间:20÷20=1小时;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
=10,CD=2×CE=2×10=20;B城处于危险区内的时间:20÷20=1小时;所以,选B。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
10、如图,已知直角梯形ABCD的上底长18厘米,下底长27厘米,高24厘米,三角形ABF、三角形ADE和四边形AECF’面积相等。三角形AEF的面积为多少平方厘米?_____ 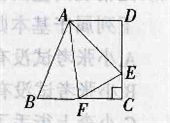
A: 165B: 132C: 160D: 156
参考答案: D 本题解释:参考答案 题目详解:依题意:
题目详解:依题意: 平方厘米;且
平方厘米;且 平方厘米;故
平方厘米;故 厘米;则
厘米;则 厘米;
厘米; 方厘米;故
方厘米;故 厘米,
厘米, 厘米,
厘米, 平方厘米;
平方厘米; 平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
平方厘米;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
11、在下列a、b、c、d四个等周长的规则几何图形中,面积最大和最小的分别是_____。 
A: a和cB: d和aC: b和dD: d和c
参考答案: D 本题解释:参考答案 题目详解:根据几何问题基本知识点:周长相同则边数越少面积也越小,越趋近圆,面积越大;依题意:a.五边形;b.正方形c.三角形d.圆形x所以,周长相同,面积最大是d;面积最小的是c;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
题目详解:根据几何问题基本知识点:周长相同则边数越少面积也越小,越趋近圆,面积越大;依题意:a.五边形;b.正方形c.三角形d.圆形x所以,周长相同,面积最大是d;面积最小的是c;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
12、有一批长度分别为3、4、5、6和7厘米的细木条,它们的数量足够多,从中适当选取3根木条作为三角形的三条边,可能围成多少个不同的三角形?_____
A: 25个B: 28个C: 30个D: 32个
参考答案: D 本题解释:参考答案 题目详解:我们分三种情况分析:(1)等边三角形:有
题目详解:我们分三种情况分析:(1)等边三角形:有 ,并且能全部围成三角形;(2)等腰非等边三角形:有
,并且能全部围成三角形;(2)等腰非等边三角形:有 ,其中3、3、7和3、3、6不能围成三角形(不能满足两边之和大于第三边),还剩下18个;(3)非等腰三角形:有
,其中3、3、7和3、3、6不能围成三角形(不能满足两边之和大于第三边),还剩下18个;(3)非等腰三角形:有 (个),其中3、4、7不能围成三角形,还剩9个。综上,满足条件的三角形一共有:5+18+9=32个。所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
(个),其中3、4、7不能围成三角形,还剩9个。综上,满足条件的三角形一共有:5+18+9=32个。所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
13、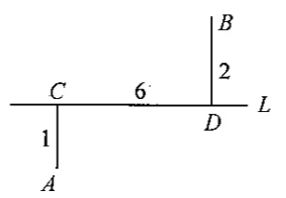
A: 2.75B: 3.25C: 2D: 3
参考答案: 本题解释:参考答案:C题目详解:由两点之间线段最短可知:连接AB,交公路L于点E,E点就是A、B两个村庄到此处处理垃圾都比较方便的地方。设CE距离为x:根据tanA=a/b可得:tanA=x/1=x,tanB=(6-x)/2=3-x/2;由于∠A=∠B:故x=3-x/2,解得,x=2。即应建在离C处2公里。所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)