时间:2021-04-05 06:41:10
1、单选题 从平面A外一点P引与A相交的直线,使得P点与交点的距离等于1,则满足条件的直线条数一定不可能是:_____
A: 0条
B: 1条
C: 2条
D: 无数条
参考答案: C
本题解释:正确答案是C考点几何问题解析当P点与平面A的垂直距离小于1时,这样的直线有无数条;当P点与平面A的垂直距离等于1时,这样的直线有1条,当P点与平面A的垂直距离大于1时,这样的直线有0条,所以不会出现有2条的情况,正确答案为C。
2、单选题 有若干人,排成一个空心的四层方阵。现在调整阵形,把最外边一层每边人数减少16人,层数由原来的四层变成八层,则共有_____人。
A: 160
B: 1296
C: 640
D: 1936
参考答案: C
本题解释:参考答案:C
题目详解:设调整前最外层每边
3、单选题 一个数被3除余1,被4除余2,被5除余4,1000以内这样的数有多少个?_____
A: 15
B: 17
C: 18
D: 19
参考答案: B
本题解释:参考答案:B
题目详解:3、4的最小公倍数为12;根据"差同减差,公倍数做周期"可知:所有满足条件的数可表示为12n-2,也就是除以12余2;所有12n-2中满足被5除余4:最小数是n=3时,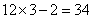
4、单选题 一篇文章,现有甲、乙、丙三人,如果由甲、乙两人合作翻译,需要10小时完成,如果由乙、丙两人合作翻译,需要12小时完成。现在先由甲、丙两人合作翻译4小时,剩下的再由乙单独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,要多少个小时完成?_____
A: 15
B: 18
C: 20
D: 25
参考答案: A
本题解释:正确答案是A考点工程问题解析设总量为1,由题意知甲乙合作的效率为1/10,乙丙合作的效率为1/12。题目给出完成该项工程的过程是甲丙先合作4个小时,乙单独翻译12个小时。在这个工作过程中,甲完成了4个小时的工作量,已完成了12个小时的工作量,丙完成了4个小时的工作量,保持此总量不变,将乙的工作拆分为三个独立的4个小时,重新为如下工作过程:甲乙先合作4个小时,乙丙再合作4个小时,最后乙单独做4个小时,仍然可以保证工程完成。于是假设乙的效率为y,可知4×1/10+4×1/12+4y=1,解得y=1/15,于是乙单独完成需要15个小时,故正确答案为A。
5、单选题 某洗车店洗车分外部清洁和内部清洁,两道工序时间均不少于30分钟,而且同一辆车两道工序不能同时进行,洗车间同一时间只能容下2辆车。现有9辆车需要清洗,汽车进出洗车间的时间可忽略不计,则洗完9辆车至少需要的时间为_____。
A: 330分钟
B: 300分钟
C: 270分钟
D: 250分钟
参考答案: C
本题解释:正确答案是C考点统筹规划问题解析前6辆车都是2辆车同时依次进行外部清洁和内部清洁,耗时60×3=180分钟。最后3辆车记为A、B、C,工作安排为A、B车外部清洁,然后B、C车内部清洁,然后A车内部清洁的同时C车外部清洁,共计耗时90分钟。因此洗完9辆车至少需要270分钟。故正确答案为C。