时间:2020-10-28 03:39:54
1、单选题 现在有64个乒乓球,18个乒乓球盒,每个盒子里最多可以放6个乒乓球,最少要放1个乒乓球,至少有几个乒乓球盒子里的乒乓球数目相同?_____
A: 4
B: 5
C: 8
D: 10
参考答案: A
本题解释:参考答案:A
题目详解:假设第一只盒子装1个乒乓球,第二只盒子装2个乒乓球,第三只盒子装3个乒乓球,第四只盒子装4个乒乓球,第五只盒子装5个乒乓球,第六只盒子装6个乒乓球。由于最多只能装6个乒乓球,所以第七到第十二也只能是这种情况,第十三到第十八也相同。第一到第六个盒子共装了21个乒乓球,第一到第十八个盒子装了21×3=63个乒乓球,此时有三个盒子装的乒乓球数量一样多。所以如果将第64个乒乓球算上,则有四个盒子装的乒乓球数量一样多。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
2、单选题 有黑色、白色、黄色的筷子各8双,混杂地放在一起,黑暗中想从这些筷子中取出颜色不同的两双筷子,问至少要取多少根才能保证达到要求?_____
A: 4
B: 5
C: 11
D: 19
参考答案: D
本题解释:参考答案
题目详解:解法一:考虑最差的情形。先选出一种颜色所有的筷子,然后再取出剩下的两种颜色的筷子各1根,最后再随便取1根即可。因此,至少要取8×2+1×2+1=19根,才能保证达到要求。解法二:1.最不好的取法是一种取了8双,另2种各取了1根,还不能保证有颜色不同的筷子两双;2.如果再取1根,在剩下的2种中,不管从哪一种取1根,都会和已经取出的凑成颜色相同的一双筷子,所以至少要取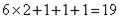
3、单选题 新年晚会上,老师让每位同学从一个装有许多玻璃球的口袋中取两个球,这些球的手感相同,只有红、黄、白、蓝、绿五色之分,结果发现总有两个人取的球相同,由此可知,参加取球的至少有多少人?_____
A: 15
B: 16
C: 17
D: 18
参考答案: B
本题解释:参考答案:B
题目详解:解法一:摸两个球,则:两球的颜色不同的情况有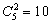
4、单选题 全班有40个同学来分819本书,每个人至少分到一本,请问,至少有几个同学分得同样多的书?_____
A: 2
B: 3
C: 4
D: 5
参考答案: A
本题解释:参考答案:A
题目详解:解法一:考虑最差情况。40个同学,如果每个人分到的书的数量都不一样多,假设第一个同学分1本,第二个同学分2本,.....那么至少应该有1+2+…+40=820本书,但现在只有819本书,也就是少了一本书,即有人少拿了一本书,因此至少有2个同学分得同样多的书。所以,选A。解法二:等差为1,首项为1,共有40项的数列的和: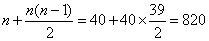
5、单选题 学校五(一)班40名学生中,年龄最大的是13岁,最小的是11岁,那么其中至少有多少名学生是同年同月出生的?_____
B: 1
C: 2
D: 3
参考答案: C
本题解释:参考答案:C
题目详解:解法一:把同年同月的放在一组里面,那么每一组可以作为1个“抽屉”;因此,可以构成3×12=36个“抽屉”,40÷36=1…4;由抽屉原理1可以得到,至少有2名学生是同年同月出生的。解法二:这40名同学的年龄最多相差36个月(三年),因40=1×36+4,故必有2人是同年、同月出生的。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1