时间:2020-01-27 03:16:12
1、单选题 甲早上从某地出发匀速前进，一段时间后，乙从同一地点出发以同样的速度同向前进，在上午10点时，乙走了6千米，他们继续前进，在乙走到甲在上午10时到达的位置时，甲共走了16.8千米，则此时乙走了_____。
A: 11.4千米
B: 14.4千米
C: 10.8千米
D: 5.4千米
参考答案: A
本题解释:正确答案是A考点行程问题解析
2、单选题 地球表面的陆地面积和海洋面积之比是29：71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____。
A: 284：29
B: 113：55
C: 371：313
D: 171：113
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：(50-29×0.25)：(50-29×0.75)=42.75：28.25=171：113。故正确答案为D。
3、单选题 如下图：已知直线P
A:y=kx+4与直线P
B:y=x+b相交于P(1，2)，且分别与x轴、y轴交于点A、B。则四边形OAPB的面积是_____。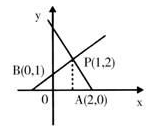
A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C解析已知P
A:y=kx+4与直线P
B:y=x+b相交于P(1，2)。则k+4=2，1+b=2，解得k=-2，b=1，故P
A:y=-2x+4，P
B:y=x+1。PB与x轴交点为(-1，0)，则底边长为2-(-1)=3。故有3×2÷2-1×1÷2=2.5，故正确答案为C。考点几何问题
4、单选题 草地上插了若干根旗杆，已知旗杆的高度在1至5米之间，且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去，在不知旗杆数量和位置的情况下，最少需要准备多少米长的绳子?_____
A: 40
B: 100
C: 60
D: 80
参考答案: D
本题解释:正确答案是D考点几何问题解析解析1：
5、单选题 自然数P满足下列条件：P除以10的余数为9，P除以9的余数为8，P除以8的余数为7。如果：100＜P＜1000，则这样的P有几个？_____
A: 不存在
B: 1个
C: 2个
D: 3个
参考答案: C
本题解释:正确答案是C解析由"
除以10的余数为9，P除以9的余数为8，P除以8的余数为7"，满足差同减差，对应口诀可知其符合表达式为360n－1，由于100＜P＜1000，则100＜360n－1＜1000，所以n能取1、2，则满足条件的P有两个，即359和719，故正确答案为C。注释：同余问题需要掌握如下口诀：余同取余，和同加和，差同加差，最小公倍数做周期。口诀解释：余同取余，例如"一个数除以7余1，除以6余1，除以5余1"，可见所得余数恒为1，则取1，被除数的表达式为210n＋1；和同加和，例如"一个数除以7余1，除以6余2，除以5余3"，可见除数与余的和相同，取此和8，被除数的表达式为210n＋8；差同减差，例如"一个数除以7余3，除以6余2，除以5余1"，可见除数与余的差相同，取此差4，被除数的表达式为210n－4。特别注意前面的210是5、6、7的最小公倍数。余数与同余问题标签同余问题