时间:2018-05-05 17:51:34
1、单选题 如下图:已知直线P
A:y=kx+4与直线P
B:y=x+b相交于P(1,2),且分别与x轴、y轴交于点A、B。则四边形OAPB的面积是_____。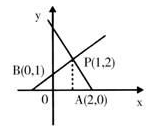 A: A
A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C解析已知P
A:y=kx+4与直线P
B:y=x+b相交于P(1,2)。则k+4=2,1+b=2,解得k=-2,b=1,故P
A:y=-2x+4,P
B:y=x+1。PB与x轴交点为(-1,0),则底边长为2-(-1)=3。故有3×2÷2-1×1÷2=2.5,故正确答案为C。考点几何问题
2、单选题 某街道常住人口与外来人口之比为1:2,已知该街道下辖的甲、乙、丙三个社区人口比为12:8:7。其中,甲社区常住人口与外来人口比为1:3,乙社区为3:5,则丙社区常住人口与外来人口比为_____。
A: 2:3
B: 1:2
C: 1:3
D: 3:4
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析根据题目中给出的比例,赋值某街道的总人数27人,则常住人口与外来人口分别为9、18人,甲、乙、丙三个社区的人口总数分别为12、8、7人。甲社区的常住人口与外来人口分别为3、9人,乙社区的常住人口与外来人口分别为3、5人,因此丙社区的常住人口与外来人口分别为3、4人。因此两者比例为3:4。故正确答案为D。标签赋值思想
3、单选题 在1000以内,除以3余2,除以7余3,除以11余4的数有多少个?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析同余问题,不符合“余同取余,和同加和,差同减差,最小公倍数做周期”的口诀,通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17,其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意:0≤231n+59≤1000,解得0≤n≤4。所以这样的数共有5个,故正确答案为B。口诀解释:余同取余,例如“一个数除以7余1,除以6余1,除以5余1”,可见所得余数恒为1,则取1,被除数的表达式为210n+1;和同加和,例如“一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如“一个数除以7余3,除以6余2,除以5余1”,可见除数与余数的差相同,取此差4,被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。
4、单选题 有一1500米的环形跑道,甲、乙二人同时同地出发,若同方向跑,50分钟后甲比乙多跑一圈,若以相反方向跑,2分钟后二人相遇,则乙的速度为_____
A: 330米/分钟
B: 360米/分钟
C: 375米/分钟
D: 390米/分钟
参考答案: B
本题解释:正确答案:B解析:依据题意:(甲的速度-乙的速度)×50=1500,(甲的速度+乙的速度)×2=1500,推出甲、乙各为390、360。故答案为B。
5、单选题 8个甲级队应邀参加比赛,先平均分成两组,分别进行单循环赛,每组决出前两名,再由每组的第一名,另一组的第二名进行淘汰赛,获胜者角逐冠、亚军,败者角逐第3、4名,整个赛程的比赛场数是_____。
A: 16
B: 15
C: 14
D: 13
参考答案: A
本题解释:正确答案是A考点计数模型问题解析