时间:2017-08-09 08:21:38
1、计算题 (18分)如图所示,k是产生带电粒子的装置,从其小孔a水平向左射出比荷为1.0×l03C/kg的不同速率的带电粒子,带电粒子的重力忽略不计.Q是速度选择器,其内有垂直纸面向里的磁感应强度为3.0×l0-3T的匀强磁场和竖直方向的匀强电场(电场线未画出).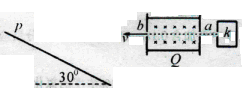
(1)测得从Q的b孔水平向左射出的带电粒子的速率为2.0×l03m/s,求Q内匀强电场场强的大小和方向.
(2)为了使从b孔射出的带电粒子垂直地打在与水平面成30°角的P屏上,可以在b孔与P屏之间加一个边界为正三角形的有界匀强磁场,磁场方向垂直纸面.试求该正三角形匀强磁场的最小面积S与磁感应强度B间所满足的关系.
参考答案:解:(1)从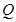 的
的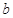 孔水平向左射出的速率为
孔水平向左射出的速率为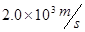 的带电粒子一定在
的带电粒子一定在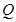 中做匀速直线运动,由平衡条件得:
中做匀速直线运动,由平衡条件得: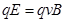 ?(1)2分
?(1)2分
可得: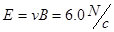 ?(2)2分
?(2)2分
由分析判断可知,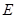 的方向竖直向上。?(3)2分
的方向竖直向上。?(3)2分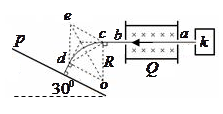
(2)设带电粒子从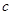 点进入磁场,从
点进入磁场,从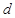 点射出磁场,带电粒子在磁场中运动的轨迹如图所示。由图可得,
点射出磁场,带电粒子在磁场中运动的轨迹如图所示。由图可得,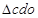 是正三角形,
是正三角形,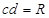 ?(4)2分
?(4)2分
由分析可知,将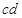 作为正三角形匀强磁场的一个边界时,正三角形匀强磁场的面积最小,所以该正三角形匀强磁场的区域如图中
作为正三角形匀强磁场的一个边界时,正三角形匀强磁场的面积最小,所以该正三角形匀强磁场的区域如图中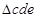 区域。?(5)2分
区域。?(5)2分
由于边长为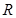 的正三角形
的正三角形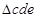 的高为
的高为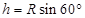 ?(6)2分
?(6)2分
边长为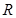 的正三角形
的正三角形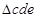 的面积为
的面积为 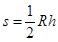 ?(7)2分
?(7)2分
又带电粒子做匀速圆周运动的轨道半径为 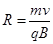 ?(8)2分
?(8)2分
由(6)、(7)、(8)解得,正三角形匀强磁场的最小面积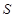 与磁感应强度
与磁感应强度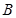 间所满足的关系:
间所满足的关系: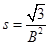 ?(9)2分
?(9)2分
本题解析:略
本题难度:一般
2、计算题 如题25图所示,在直角坐标xOy平面y轴左侧(含y轴)有一沿y轴负向的匀强电场,一质量为m,电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场,从y轴上Q点离开电场时速度方向与y轴负向夹角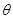 =30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小
=30°,Q点坐标为(0,-d),在y轴右侧有一与坐标平面垂直的有界匀强磁场区域(图中未画出),磁场磁感应强度大小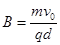 ,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求:
,粒子能从坐标原点O沿x轴负向再进入电场.不计粒子重力,求: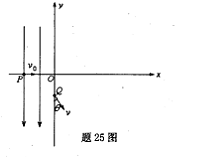
(1)电场强度大小E;
(2)如果有界匀强磁场区域为半圆形,求磁场区域的最小面积;
(3)粒子从P点运动到O点的总时间.
参考答案:(1)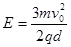 (2)
(2)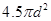 (3)
(3)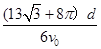
本题解析:首先根据平抛运动及动能定理求出电场强度;画出运动轨迹,求出半径,根据几何关系求出最小面积;分步求出各段的时间,最后求和得出总时间。
(1)设粒子从Q点离开电场时速度大小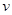
由粒子在匀强电场中做类平抛运动得: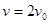 (1分)
(1分)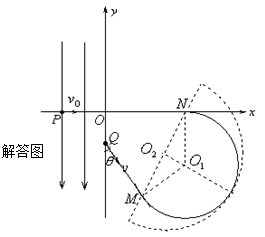
由动能定理得?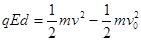 ?(2分)
?(2分)
解得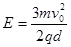 (1分)
(1分)
(2)设粒子从M点进入、N点离开半圆形匀强磁场区域
粒子在磁场中做匀速圆周运动半径为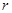 ,圆心为
,圆心为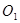 ,如解答图所示
,如解答图所示
由洛伦兹力提供向心力,得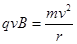 ?
?
解得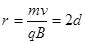 (2分)
(2分)
若半圆形磁场区域的面积最小,则半圆形磁场区域的圆心为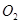
可得半径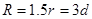 (2分)半圆形磁场区域的最小面积
(2分)半圆形磁场区域的最小面积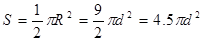 (2分)
(2分)
(3)设粒子在匀强电场中运动时间为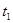
粒子从Q点离开电场时沿y轴负向速度大小为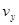 ?有
?有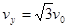
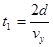 ?解得
?解得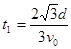 (2分)
(2分)
设粒子在磁场中做匀速圆周运动时间为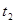 ?有
?有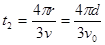 (2分)
(2分)
粒子在QM、NO间做匀速直线运动时间分别为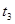 、
、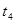
由几何关系可得QM距离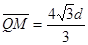 ?得
?得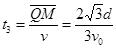 (2分)
(2分)
NO间距离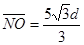 ?得
?得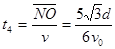 (2分)
(2分)
粒子从P点运动到O点的总时间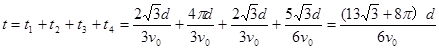 (1分)
(1分)
本题难度:一般
3、选择题 如图所示,L1和L2是输电线,甲是电压互感器,乙是电流互感器。若已知甲的变压比为1000:1,乙的变流比为100:l,并且已知加在电压表两端的电压为220V,通过电流表的电流为10A,则输电线的输送功率为(?)?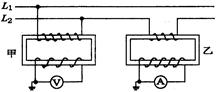
A.2.2×103W
B.2.2×10-2W
C.2.2×l08W
D.2.2×104W
参考答案:C
本题解析:依题输送电压为2.2×l05V,输送电流为1×103V
本题难度:简单
4、计算题 如图所示,一个质量为m,电量为q的带正电的粒子(不计重力),从静止开始经电压U加速后,沿水平方向进入一宽度为L的区域中,当在该区域内同时施加垂直于纸面向里的匀强磁场和竖直向下的匀强电场时,粒子恰好沿水平方向做直线运动,从O点射出该区域的右边界;若去掉电场只保留磁场,该粒子仍从静止经电压U加速后沿水平方向进入这一区域,恰好从C点射出该区域的右边界,且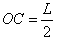 。
。
(1)求磁场的磁感应强度B的大小;
(2)如果去掉磁场只保留电场,该粒子仍从静止经电压U加速后沿水平方向进入这一区域,粒子在该区域右边界的射出点离O点的距离为多少? 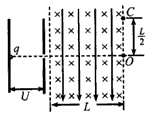
参考答案:解:(1)粒子经过加速电场,由动能定理得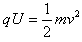 ①
①
由图可得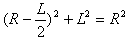 ?②
?②
得 ?③
?③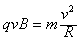 ?④
?④
由①②③④式得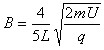 ?⑤
?⑤ 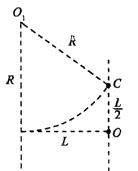
(2)在电场和磁场同时存在时qvB=Eq ⑥
只剩余电场时,时间 ⑦
⑦
侧移量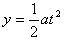 ?⑧
?⑧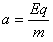 ?⑨
?⑨
由①⑤⑥⑦⑧⑨式得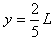 ?⑩
?⑩
本题解析:
本题难度:困难
5、选择题 .一个带电粒子处于垂直于匀强磁场方向的平面内,只在磁场力的作用下做匀速圆周运动.要想确定带电粒子的电荷量与质量之比,则只需要知道
A.运动速度v和磁感应强度B
B.轨道半径R和磁感应强度B
C.轨道半径R和运动速度v
D.磁感应强度B和运动周期T
参考答案:D
本题解析:此题涉及带点粒子在磁场中的运动。带电粒子在磁场中的运动时,洛伦兹力提供向心力,可以得到公式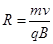 和
和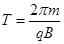 ,有公式可以看出,测出电荷量与质量之比可以知道运动速度v、轨道半径R和磁感应强度B或者知道.磁感应强度B和运动周期T 。所以答案选D。本题考查了带点粒子在磁场中的运动的基本公式。题目简单。
,有公式可以看出,测出电荷量与质量之比可以知道运动速度v、轨道半径R和磁感应强度B或者知道.磁感应强度B和运动周期T 。所以答案选D。本题考查了带点粒子在磁场中的运动的基本公式。题目简单。
本题难度:简单