时间:2017-08-09 08:07:03
1、简答题 如图所示，在xoy平面第Ⅰ象限有匀强电场，场强大小未知，其方向沿y轴正向；在第Ⅱ象限有垂直纸面向里的匀强磁场，磁感应强度为B；P处有一放射源，内装放射性物质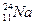
，发生衰变生成新核
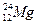，放出一个质量为m，电荷量为－q的带电粒子。带电粒子从P孔以初速度v0沿垂直于磁场方向进入匀强磁场中，初速度方向与－x轴的夹角θ=60°，粒子恰好从C孔垂直于y轴射入匀强电场，最后打在Q点，已知OQ=2OC，不计粒子的重力，
（1）写出发生衰变时的核反应方程
（2）求粒子从P运动到Q所用的时间t
（3）求粒子到达Q点的动能EkQ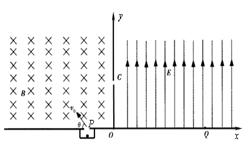
参考答案：（1）→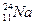
＋
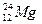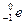（2）（3＋
）
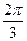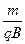（3）EKQ=mv02
本题解析：（1）放射性物质发生衰变的核反应方程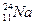→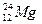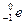＋ （3分）
（2）设带电粒子在磁场中做匀速圆周运动的半径为R，由圆周运动知识得：
qv0B＝m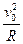
? R＝
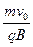①
由几何关系得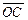
＝R＋Rcosθ ②
带电粒子在磁场中运动的时间t1＝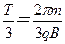
?
③
带电粒子在电场中做类平抛运动，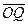
＝2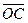
＝v0t2，
带电粒子在电场中运动的时间t2＝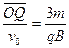
④
粒子由P运动到Q的时间t=t1+t2=（3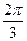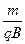＋） ⑤
（3）设电场强度为E，粒子在电场中沿电场方向做匀加速直线运动
由S＝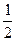
at2得?＝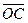
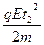，解得：E=
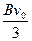⑥
根据动能定理，粒子到达Q点时的动能EKQ：
qE·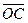=EKQ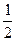－mv02 EKQ=mv02 ⑦
第①～⑥式各2分，第⑦式3分。
本题难度：一般
2、选择题 一带电粒子以初速度v0沿垂直于电场线和磁感线的方向，先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场和匀强磁场，如图甲所示。电场和磁场对粒子做功为W1，粒子穿出磁场时的速度为v1；若把电场和磁场正交叠加，如图乙所示。粒子仍以初速度v0穿过叠加场区，电场和磁场对粒子做功为W2，粒子穿出场区时的速度为v2。比较W1和W2、v1和v2的大小（v0＜E/B，不计重力）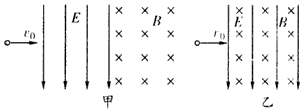 
[? ]
A．W1>W2，v1>v2
B．W1=W2，v1=v2
C．W1＜W2，v1＜v2
D．W1=W2，v1>v2
参考答案：A
本题解析：
本题难度：一般
3、选择题 如图所示，真空中存在竖直向上的匀强电场和水平方向的匀强磁场，一质量为m、带电荷量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动，下列说法正确的是（ ）
A．电场强度为
| mg q |
| qR mv |
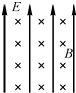
参考答案：A、磁场方向向里，洛伦兹力的方向始终指向圆心，由左手定则可判断液滴的旋转方向为逆时针；由液滴做匀速圆周运动，得知电场力和重力大小相等，得：
mg=qE…①
得：m=qEg，故A正确；
B、液滴在重力场、匀强电场和匀强磁场中做匀速圆周运动，可知，液滴受到的重力和电场力是一对平衡力，因此电场力做功，则物体运动中机械能不守恒，故B错误；
C、重力竖直向下，所以电场力竖直向上，与电场方向相同，故可知液滴带正电，根据左手定则可知，物体逆时针转动，故C正确．
D、液滴在洛伦兹力的作用下做匀速圆周运动的半径为：R=mvqB
因此磁感应强度为：B=mvqR，故D错误；
故选：AC
本题解析：
本题难度：简单
4、简答题 如图所示，虚线上方有场强为E1＝6×104N/C的匀强电场，方向竖直向上，虚线下方有场强为E2的匀强电场，电场线用实线表示，另外，在虚线上、下方均有匀强磁场，磁感应强度相等，方向垂直纸面向里，ab是一长为L＝0.3m的绝缘细杆，沿E1电场线方向放置在虚线上方的电、磁场中，b端在虚线上，将一套在ab杆上的带电量为q＝－5×10－8C的带电小环从a端由静止释放后，小环先作加速运动而后作匀速运动到达b端，小环与杆间的动摩擦因数μ＝0.25，不计小环的重力，小环脱离ab杆后在虚线下方仍沿原方向作匀速直线运动．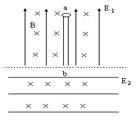
(1)请指明匀强电场E2的场强方向，说明理由，并计算出场强E2的大小；
(2)若撤去虚线下方电场E2，其他条件不变，小环进入虚线下方区域后运动轨迹是半径为L/3的半圆，小环从a到b的运动过程中克服摩擦力做的功为多少？
?
参考答案：（1）电场方向向左，2.4×105N/C
（2）－3×10－4J
本题解析：设匀强磁场的磁感应强度为B，带电粒子在虚线上方匀速运动速度为V，
(1)带电小环在虚线上方做匀速运动时，有
μBvq＝qE1 (1)
带电小环在虚线下方做匀速运动，洛仑兹力的方向向左，由于小环做匀速运动，可知电场力方向应向右，电场方向向左
Bvq＝qE2 (2)
解(1)、(2)得，E2＝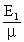
＝
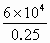N/C＝2.4×105N/C
(2)若去掉虚线下方的电场后，带电小环做圆围运动，有
? Bvq＝m
(3)
得?
mV2＝×
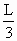×Bvq＝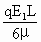
在虚线上方，电场力做功 
＝qE1L
根据动能定理 ＋Wf＝mV2－0
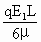? Wf＝mV2－＝mV2－qE1L＝－qE1L
＝(
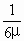－1)qE1L＝(
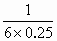－1)×6×104×5×10－8×0.3J
＝－3×10－4J
本题难度：一般
5、计算题 如图所示，在匀强电场中建立直角坐标系xoy，y轴竖直向上，一质量为m、电荷量为+q的微粒从x轴上的M点射出,方向与x轴夹角为θ,微粒恰能以速度v做匀速直线
运动,重力加速度为g。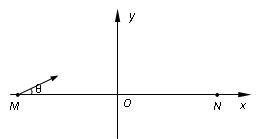
（1）求匀强电场场强E的大小及方向；
（2）若再叠加一圆形边界的匀强磁场,使微粒能到达x轴上的N点，M、N两点关于原点o对称，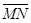
=L，微粒运动轨迹也关于y轴对称。 己知所叠加磁场的磁感应强度大小为B，方向 垂直xoy平面向外。求磁场区域的最小面积S 及微粒从M运动到N的时间t。
参考答案：(1）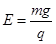
竖直向上(2）
?
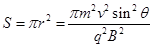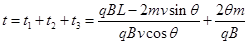
本题解析：
（1）当微粒在电场中做匀速直线运动时，它所爱的电场力与重力平衡。所以有：qE－mg=0?①（2分）
由①式可解得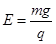：?②（1分）
E的方向竖直向上 （1分）
（2） 微粒在磁场中运动，由洛仑兹力和向心力公式得：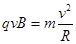
?③（2分）
由③式得：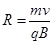
?④
如图所示，当PQ为圆形磁场的直径时，圆形磁场面积最小。（3分）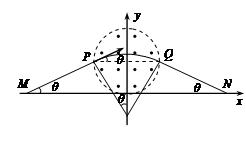
由几何知识可得：r=Rsinθ?⑤（2分）
其面积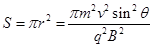?⑥
又由圆周运动规律可得：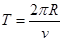
?⑦ （1分）
根据几何关系可知偏转角为2θ，则在磁场中运动的时间：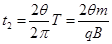
?⑧（2分）
又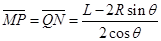
?⑨（1分）
且有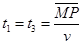
?⑩（1分）
故微粒从M运动到N的时间：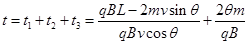
?（11） （2分）
本题难度：一般