时间:2017-08-09 07:42:16
1、计算题 (18分)如图a所示,水平直线MN下方有竖直向上的匀强电场,现将一重力不计、比荷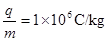 的正电荷置于电场中的O点由静止释放,经过
的正电荷置于电场中的O点由静止释放,经过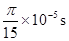 后,电荷以
后,电荷以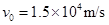 的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).计算结果可用π表示。
的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).计算结果可用π表示。
(1)求O点与直线MN之间的电势差;
(2)求图b中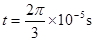 时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;
(3)如果在O点右方d=67.5cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间。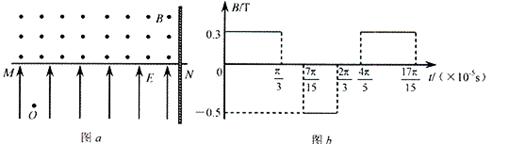
参考答案:(1)112.5V;?(2)4cm;(3) (12π+13π/45)×10-5s
本题解析:(1)电荷在电场中做匀加速直线运动,由动能定理uq=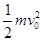 ,
,
u=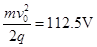
(2)当磁场垂直纸面向外时,设电荷运动的半径为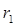 :
:
由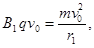 得
得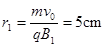 ,
,
周期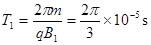 ?;
?;
当磁场垂直纸面向里时,电荷运动的半径为: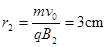 ,
,
周期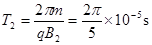
故电荷从t=0时刻开始做周期性运动,其运动轨迹如图甲所示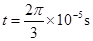 时刻电荷与O点的水平距离
时刻电荷与O点的水平距离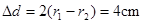 ?--?
?--?
(3)电荷第一次通过MN开始,其运动的周期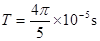 ,
,
根据电荷的运动情况可知,电荷到达挡板前运动的完整周期数为15个,
此时电荷沿MN运动的距离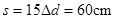 ,
,
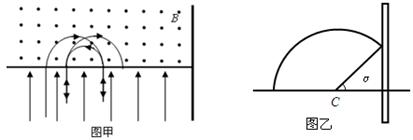
则最后7.5cm的距离如图乙所示,有: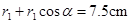 。
。
解得: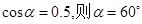 ,
,
故电荷运动的总时间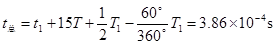 或(553π/45)×10-5s或(12π+13π/45)×10-5s
或(553π/45)×10-5s或(12π+13π/45)×10-5s
本题难度:一般
2、计算题 如图所示,坐标系中第一象限有垂直纸面向外的匀强磁场,磁感应强度B=102 T,同时有竖直向上与y轴同方向的匀强电场,场强大小E1=102 V/m,第四象限有竖直向上与y轴同方向的匀强电场,场强大小E2=2E1=2×102 V/m。若有一个带正电的微粒,质量m=10-12 kg,电量q=10-13 C,以水平与x轴同方向的初速度从坐标轴的P1点射入第四象限,OP1=0.2 m,然后从x轴上的P2点穿入第一象限,OP2=0.4 m,接着继续运动。取g=10 m/s2。求:
(1)微粒射入的初速度;
(2)微粒第三次过x轴的位置;
(3)从P1开始到第三次过x轴的总时间。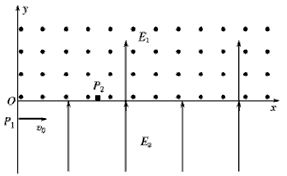
参考答案:解:(1)微粒从P1到P2做类平抛运动,由于qE2=2mg,则加速度a=g,则运动时间t1=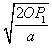 =0.2 s
=0.2 s
微粒射入的初速度:v0=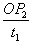 =2 m/s
=2 m/s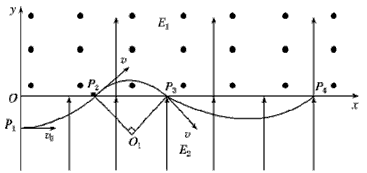
(2)微粒进入第一象限的速度:v=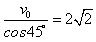 m/s
m/s
粒子运动方向与x轴夹角为45°
由qE1=mg,则微粒进入第一象限做匀速圆周运动,则圆周运动的半径R=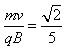 m
m
P2P3=2Rcos45°=0.4 m
圆周运动的时间t2=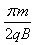 =0.157 s
=0.157 s
微粒再次进入第四象限做类斜上抛运动,由运动的分解可知:x轴方向做匀速运动,y轴方向做类上抛运动,粒子的运动时间t3=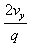 =0.4 s
=0.4 s
运动距离P3P4=vxt3=0.8 m
故OP4=OP2+P2P3+P3P4=1.6 m
微粒第三次过x轴的位置距O点1.6 m处
(3)求(2)知t=t1+t2+t3=0.757 s
本题解析:
本题难度:困难
3、计算题 如图所示,在直角坐标系Oxy平面的第三、四象限内分别存在着垂直于Oxy平面的匀强磁场,第三象限的磁感应强度大小是第四象限的2倍,方向相反。质量、电荷量相同的负粒子a、b,某时刻以大小相同的速度分别从x轴上的P、Q两点沿y轴负方向垂直射入第四、三象限磁场区域。已知a粒子在离开第四象限磁场时,速度方向与y轴的夹角为60o,且a在第四象限磁场中运行时间是b粒子在第三象限磁场中运行时间的4倍。不计重力和两粒子之间的相互作用力。求: a、b两粒子经Y轴时距原点O的距离之比。
参考答案:a、b两粒子经Y轴时距距原点O的距离之比为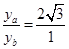
本题解析:
试题分析:学设第三象限内磁场磁感应强度大小为2B,第四象限内磁场磁感应强度大小为B,粒子a、b质量为m电荷量大小为q进入磁场区域速度为v由洛伦兹力和牛顿第二定律得: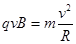 ?
?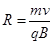 ?
?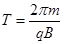
由题设条件有: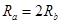 ?
?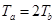
设b粒子在第三象限中运行时转过的圆心角为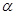 ,由a、b两粒子运行时间关系有:
,由a、b两粒子运行时间关系有: 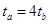 ?即
?即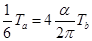 ?得
?得 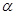 =30?
=30?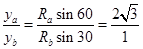 考点:
考点:
本题难度:一般
4、计算题 (10分)在相互垂直的匀强电场和匀强磁场中,有一倾角为θ,足够长的光滑绝缘斜面,磁感应强度为B,方向垂直纸面向外,电场方向竖直向上。有一质量为m,带电荷量为+q的小球静止在斜面顶端,这时小球对斜面的正压力恰好为零,如图所示,若迅速把电场方向反转成竖直向下。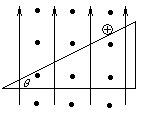
求:
(1)小球能在斜面上连续滑行多远?
(2)所用时间是多少?
参考答案:(1)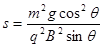 ?(2)
?(2)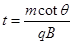
本题解析:(1)电场反转前mg=qE?
电场反转后,小球先沿斜面向下做匀加速直线运动,到对斜面压力减为零时开始离开斜面,此时有: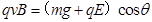 ?
?
解得小球离开斜面时的速度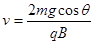 ?
?
小球在斜面上滑行的加速度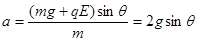
小球在斜面上滑行的距离为: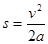 ?
?
小球沿斜面滑行距离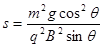
(2)所用时间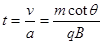 ?
?
点评:此类题型关键在与分析题目所给已知信息,利用正交分解法结合牛顿运动定律分析出离开斜面条件,进而利用匀变速直线运动规律求解。
本题难度:一般
5、计算题 如图,在平面直角坐标系xOy内,第1象限存在沿y轴负方向的匀强电场,第Ⅳ象限以ON为直径的半圆形区域内,存在垂直于坐标平面向外的匀强磁场,磁感应强度为B。一质量为m、电荷量为q的带正电的粒子,从y轴正半轴上y=h处的M点,以速度v0垂直于y轴射入电场,经x轴上x=2h处的P点进入磁场,最后以垂直于y轴的方向射出磁场。不计粒子重力。求:
(1)电场强度大小E;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从进入电场到离开磁场经历的总时间t。 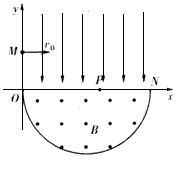
参考答案:解:粒子的运动轨迹如下图所示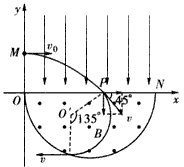 ?
?
(1)设粒子在电场中运动的时间为t1,则 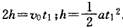
根据牛顿第二定律Eq=ma
求出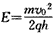
(2)根据动能定理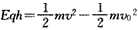
设粒子进入磁场时速度为v,根据牛顿第二定律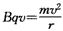
求得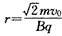
(3)粒子在电场中运动的时间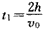
粒子在磁场中运动的周期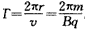
设粒子在磁场中运动的时间为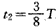
求得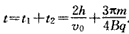
本题解析:
本题难度:困难