时间:2017-08-09 07:40:48
1、简答题 如图，水平轨道AB与半径为R=1.0m的竖直半圆形光滑轨道BC相切于B点．可视为质点的a、b两个小滑块质量ma=2mb=2kg，原来静止于水平轨道A处，AB长为L=3.2m，两滑块在足够大的内力作用下突然分开，已知a、b两滑块分别沿AB轨道向左右运动，va=4.5m/s，b滑块与水平面间动摩擦因数μ=0.5，g取10m/s2．则
（1）小滑块b经过圆形轨道的B点时对轨道的压力．
（2）通过计算说明小滑块b能否到达圆形轨道的最高点C．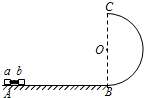
参考答案：（1）系统的动量守恒可得mava=mbvb，①
又ma=2mb=2?kg，va=4.5m/s
解得：vb=9.0m/s?②
设滑块b到达B点时的速度为vB，由动能定理得，-μmbgL=12mbv2B-12mbv2b③
刚进入圆轨道时，设滑块b受到的支持力为FN，由牛顿第二定律得，FN-mbg=mbv2BR④
由牛顿第三定律FN=-F′N⑤
由③④⑤得滑块b对轨道的压力F′N=-59N，方向竖直向下
（2）若小滑块b能到达圆轨道最高点，速度为vC
则由机械能守恒，12mbv2B=mbg2R+12mbv2C⑥
解得vc=3.0m/s⑦
小物块b恰能过最高点的速度为v，则mbg=mbv2?R⑧
解得，v=
本题解析：
本题难度：一般
2、简答题 如图所示，竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切，圆弧轨道的半径为R，圆心O与A、D在同一水平面上，∠COB=θ，现有质量为m的小物体从距D点为
| Rcosθ 4 |
| sinθ 2cosθ |
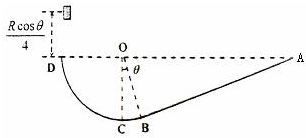
参考答案：（1）为使小物体不会从A点冲出斜面，由动能定理得mgRcosθ4-μmgcosθRcosθsinθ=0
解得动摩擦因数至少为：μ=sinθ4cosθ
（2）分析运动过程可得，最终小物体将从B点开始做往复的运动，由动能定理得
mg（Rcosθ4+Rcosθ）-μmgScosθ=0
解得小物体在斜面上通过的总路程为：S=5Rcosθ2sinθ
（3）由于小物体第一次通过最低点时速度最大，此时压力最大，由动能定理，得
mg（Rcosθ4+R）=12mv2
由牛顿第二定律，得
Nmax-mg=mv2R
解得Nmax=3mg+12mgcosθ
最终小物体将从B点开始做往复的运动，则有
mgR（1-cosθ）=12mv′2
Nmin-mg=mv′2R
联立以上两式解得Nmin=mg（3-2cosθ）
由牛顿第三定律，得小物体通过圆弧轨道最低点C时对C的最大压力
Nmax′=3mg+12mgcosθ，
最小压力Nmin′=mg（3-2cosθ）．
本题解析：
本题难度：一般
3、计算题 （13分）如图所示，传送带以一定速度沿水平方向匀速运动，将质量m＝1.0kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧的两端点，其连线水平，轨道最低点为O，已知圆弧对应圆心角θ＝106°，圆弧半径R＝1.0m，A点距水平面的高度h＝0.8m，小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动，经过 0.8s小物块经过D点，已知小物块与斜面间的动摩擦因数μ＝.(取sin53°＝0.8，g＝10m/s2)求：
?
(1)小物块离开A点时的水平速度大小；
(2)小物块经过O点时，轨道对它的支持力大小；
(3)斜面上C、D间的距离．
参考答案：(1) vA＝3m/s? (2) FN＝43N? (3) 0.98m.
本题解析：(1)对于小物块，由A到B做平抛运动，在竖直方向上有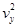
＝2gh①
在B点时有tan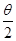
＝
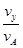②
由①②解得vA＝3m/s
(2)小物块在B点的速度为vB＝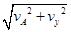
＝5m/s
由B到O由动能定理(或机械能守恒定律)得
mgR(1－sin37°)＝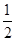
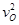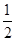m
－m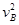
由牛顿第二定律得FN－mg＝m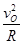
解得FN＝43N
(3)物块沿斜面上滑时，有mgsin53°＋μmgcos53°＝ma1
vC＝vB＝5m/s
小物块由C上升到最高点的时间为t1＝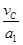
＝0.5s
则小物块由斜面最高点回到D点历时
t2＝0.8s－0.5s＝0.3s
小物 91ExAM.org块沿斜面下滑时，由牛顿第二定律得
mgsin53°－μmgcos53°＝ma2
C、D间的距离为xCD＝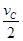
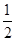t1－a2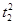
?＝0.98m.
本题难度：一般
4、选择题 一个质量为m的人站在电梯中，电梯加速上升，加速度大小为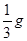
，g为重力加速度，人对电梯的压力为（?）
A．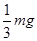
B．2mg
C．mg
D．
参考答案：D
本题解析：在竖直方向上人受到竖直向下的重力，竖直向上的支持力，所以根据牛顿第二运动定律可得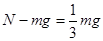
，即电梯对人的支持力为，因为电梯对人的支持力与人对电梯的压力是一对相互作用力，所以人对电梯的压力为
D正确。
本题难度：简单
5、填空题 如图，在光滑水平面上固定三个等质量的带电小球（均可视为质点），A、B、C三球排成一直线．若释放A球（另两球仍固定）的瞬时，A球的加速度大小为1m/s2，方向向左；若释放C球（另两球仍固定）的瞬时，C球的加速度大小为2m/s2，方向向右；则释放B的瞬时，B球的加速度大小为______m/s2，方向向______．
参考答案：
小球A受到小球B和C的作用力分别记为FBA和FCA，小球B分别受到小球A和C的作用力分别记为FAB和FCB，小球C受到A和B的作用力记为FAC和FBC
对小球A有：FBA+FCA=ma1? ①
对小球B有：FAB+FCB=ma2? ②
对小球C有：FAC+FBC=ma3? ③
由于FBA和FAB互为作用力和反作用力，故其大小相等方向相反，有FBA+FAB=0，故有
①+②+③得：
ma1+ma2+ma3=0
根据题意取向左为正方向，则有：a1=1m/s2，a3=-2m/s2
据ma1+ma2+ma3=0知a2=1m/s2，方向与正方向相同即向左．
即释放B球时，B球的加速度大小为1m/s2，方向向左．
故答案为：1，左．
本题解析：
本题难度：一般