时间:2017-08-07 16:23:30
1、简答题 右图是一个设计“过山车”的试验装置的工作原理示意图，光滑斜面与竖直平面内的圆形轨道的最低点B平滑连接，圆形轨道半径为R，一质量为m的小车(可视为质点)在A点由静止释放并沿斜面滑下，当小车第一次经过B点进入圆形轨道时对轨道B点的压力为其所受重力的7倍，小车恰能越过圆形轨道最高点C完成圆周运动并第二次经过最低点B再沿水平轨道向右运动。已知重力加速度的大小为g。
(1)求A点距水平面的高度h；
(2)假设小车在竖直圆轨道的左、右半圆轨道部分克服摩擦阻力做功相等，求小车第二次经过 圆轨道最低点B时速度有多大?
参考答案：（1）
（2）
本题解析：（1）依题意，在B点应用牛顿第二定律有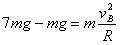
?…………………①（３分）
由机械能守恒定律有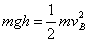
?………………②（３分）
由①、②两式解得A点距水平面的高度为：?…………③（２分）
（2）依题意，在C点应用牛顿第二定律有：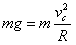
?………………………④（３分）
则小车从B到C的过程中，克服摩擦阻力做功为
?……………⑤（３分）
从C到B的过程中应用动能定理有
?………………………⑥（３分）
解得小车第二次经过圆轨道最低点B时的速度为：
′＝?…………………⑦（２分）
本题难度：一般
2、简答题 光具有波粒二象性，光子能量E=hν，其中频率ν表征波的特征，在爱因斯坦提出光子说之后，法国物理学家德布罗意提出了光子动量p与光波波长λ的关系是p=h/λ，若某激光管以Pw=60W的功率发射波长λ=6.63×10-7m的光，试根据上述理论计算：
（1）该管在1min内发射多少个光子？（普朗克常量h=6.63×10-34J-s）
（2）若光束全部被某黑体表面吸收，那么该黑体表面所受到光束对它的作用力为多大？
参考答案：（1）激光管在1min内发射光子的个数为
n=Pwthcλ=Pwtλhc=60×6.63×10-7×606.63×10-34×3×108=1.2×1022个．
（2）在时间△t=1min内黑体获得总冲量为F?△t，由动量定理得，F?△t=np
即：F=np△t=nhλ△t=1.20×1022×6.63×10-346.63×10-7×60=2×10-7N．
答：（1）该管在1min内发射1.2×1022个光子．
（2）若光束全部被某黑体表面吸收，那么该黑体表面所受到光束对它的作用力为2×10-7N．
本题解析：
本题难度：一般
3、选择题 质量分别为2m和m的A、B两个质点，初速度相同，均为v1。若他们分别受到相同的冲量I作用后，A的速度为v2，B的动量为p.已知A、B都做直线运动，则动量p可以表示为（ ）
A． m（v2－v1） B．2m（2v2－v1） C．4m（v2－v1） D．m（2v2－v1）
参考答案：D
本题解析：对A由动 量定理：
，对B来说：
，
则
，选项D 正确。
考点：动量定理的应用。
本题难度：一般
4、简答题 两块厚度不同的木板并在一起，直立固定在地面上。一颗子弹水平射向木板，恰好把这两块木板射穿。已知它通过这两块木板所用时间之比为1：2，并且子弹通过这两块木板时受到的阻力大小相等，求这两块木板的厚度之比。
参考答案：
5：4
本题解析：
设子弹初速度为v0, 子弹刚射穿第一块木板时速度为v1, 则
I1：I2=Δp1：Δp2=m(v0-v1)：m(v1-0)=1：2，
可解出 v1=2 v0/3。
因为 s=Δv/2a, 因此
。
本题也可以运用初速为零的匀变速直线运动的规律求解：倒过来看，它的运动就是初速为零的匀变速直线运动，相邻相等时间间隔内的位移之比为1：3：5：………现在后一块木板占两份时间，第一块木板占一份时间，因此两块木板的厚度之比为5：（3+1）=5：4。
本题难度：简单
5、选择题 a、b、c三个物体质量分别为m，2m，3m，它们在水平路面上某时刻运动的动能相等．当每个物体受到大小相同的制动力时，它们制动距离之比是
A.1∶2∶3
B.12∶22∶32
C.1∶1∶1
D.3∶2∶1
参考答案：C
本题解析：
本题难度：困难