时间:2017-08-07 16:00:55
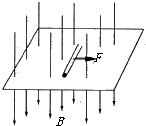
1、填空题 在操场上,两同学相距L为10m左右,在东偏北、西偏南11°的沿垂直于地磁场方向的两个位置上,面对面将一并联铜芯双绞线,象甩跳绳一样摇动,并将线的两端分别接在灵敏电流计上.双绞线并联后的电阻R为2Ω,绳摇动的频率配合节拍器的节奏,保持f=2Hz.如果同学摇动绳子的最大圆半径h=1m,电流计的最大值I=3mA.
(1)磁感应强度的数学表达式B=______.(用R,I,L,f,h等已知量表示)试估算地磁场的磁感应强度的数量级______T.
(2)将两人的位置改为与刚才方向垂直的两点上,那么电流计的读数______.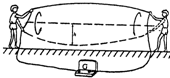
2、选择题 一直升机停在南半球的地磁极上空,该处地磁场的方向竖直向上,磁感应强度为B.直升机螺旋桨叶片的长度为l,螺旋桨转动的频率为f,顺着地磁场的方向看螺旋桨,螺旋桨按顺时针方向转动。螺旋桨叶片的近轴端为a,远轴端为b,如图所示。如果忽略a到转轴中心线的距离,用ε表示每个叶片中的感应电动势,则
[? ]
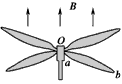
3、选择题 如图所示,一闭合的小金属环用一根绝缘细杆挂在固定点O处,使金属圆环在竖直线OO′的两侧来回摆动的过程中穿过水平方向的匀强磁场区域,磁感线的方向和水平面垂直.若悬点摩擦和空气阻力均不计,则( )
A.金属环进入和离开磁场区域都有感应电流,而且感应电流的方向相反
B.金属环进入磁场区域后越靠近OO′线时速度越大,而且产生的感应电流越大
C.金属环开始摆动后,摆角会越来越小,摆角小到某一值后不再减小
D.金属环在摆动过程中,机械能将完全转化为环中的电能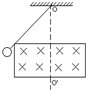
4、简答题 如图所示,一导线弯成半径为a的半圆形闭合回路.虚线MN右侧有磁感应强度为B的匀强磁场.方向垂直于回路所在的平面.回路以速度v向右匀速进入磁场,直径CD始终与MN垂直.从D点到达边界开始到C点进入磁场为止,求此过程中:
(1)感应电流方向
(2)感应电动势最大值
(3)感应电动势平均值.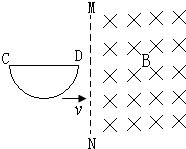
5、选择题 如图所示,匀强磁场的方向竖直向下,磁场中有光滑的水平桌面,在桌面上平放着内壁光滑、底部有带电小球的试管.在水平拉力F的作用下,试管向右匀速运动,带电小球能从试管口处飞出,则( )
A.小球带负电
B.小球运动的轨迹是一条抛物线
C.洛伦兹力对小球做正功
D.维持试管匀速运动的拉力F应逐渐增大