时间:2017-08-07 15:54:59
1、选择题 如图所示,运动员驾驶摩托车跨越壕沟,壕沟两侧的高度差为0.8m.假设运动员跨越前沿水平路面行驶,则运动员跨过壕沟时在空中飞行的时间为(取g=10m/s2)( )
A.3.2s
B.1.6s
C.0.8s
D.0.4s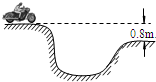
2、填空题 如图所示为一小球作平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm,g=10m/s2,那么:
(1)闪光频率为_____________Hz;
(2)小球运动的初速度的大小是____________m/s;
(3)小球经过B点时的速度大小为____________m/s。 
3、简答题 如图所示,一个人用一根长1m,只能承受46N拉力的绳子,拴着一个质量为1㎏的小球,在竖直平面内作圆周运动,已知圆心O离地面h=6m.转动中小球在最底点时绳子断了,(g=10m/s2)求:
(1)绳子断时小球运动的线速度多大?
(2)绳断后,小球落地点与抛出点间的水平距离.
4、选择题 将小球从高为20m的地方以3m/s的速度水平抛出,小球在空中的运动时间为(g=10m/s2)( )
A.1s
B.2s
C.3s
D.4s
5、选择题 将一物体从高h处以初速v0水平抛出,空气阻力不计。物体的水平射程为s,落地速度大小为v1,则其飞行时间为
[? ]
A.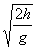
B.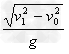
C.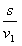
D.