时间:2017-08-07 15:35:54
1、计算题 【物理——选修3—5】(15分)
(1)(5分)下列说法正确的是?。
A.根据E=mc2可知物体所具有的能量和它的质量之间存在着简单的正比关系
B.在单缝衍射实验中,假设只让一个光子通过单缝,则该光 子不可能落在暗条纹处
子不可能落在暗条纹处
C.一群氢原子从n=3的激发态向较低能级跃迁,最多可放出二种频率的光子
D.已知能使某金属发生光电效应的极限频率为ν0,则当频率为2ν0的单色光照射该金属时,光电子的最大初动能为2hν0
(2)(10分)如图,车厢的质量为M,长度为L,静上在光滑水平面上,质量为m的木块(可看成质点)以v0的速度无摩擦地在车厢底板上向右运动,木块与前车壁碰撞后以v0/2向左运动,则再经过多长时间,木块将与后车壁相碰?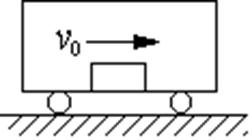
2、计算题 1919年,卢瑟福用α粒子轰击氮核发现质子。科学研究表明其核反应过程是:α粒子轰击静止的氮核后形成了不稳定的复核,复核发生衰变放出质子,变成氧核。设α粒子质量为m1,初速度为v0,氮核质量为m2,质子质量为m0,氧核质量为m3,不考虑相对论效应。
(1)α粒子轰击氮核形成不稳定复核的瞬间,复核的速度为多大?
(2)求此过程中释放的核能。
3、计算题 如图所示,质量m1=0.3 kg的小车静止在光滑的水平面上,车长L=15 m,现有质量m2=0.2 kg可视为质点的物块,以水平向右的速度v0=2 m/s从左端滑上小车,最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数μ=0.5,取g=10 m/s2。求
(1)物块在车面上滑行的时间t;
(2)要使物块不从小车右端滑出,物块滑上小车左端的速度v0′不超过多少?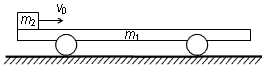
4、选择题 如图所示,木块放在光滑水平面上,一颗子弹水平射入木块中,子弹受到的平均阻力为f,射入深度为d,此过程中木块位移为s,则(?)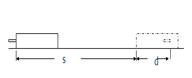
A.子弹损失的动能为fs
B.木块增加的动能为f(s+d)
C.子弹动能的减少等于木块动能的增加
D.子弹、木块系统总机械能的损失为fd
5、简答题 在光滑水平面上放置一宽度为D,电阻不计的光滑固定金属导轨,在直导轨所在的有限区域内存在垂直导轨向下的匀强磁场。垂直导轨横放着质量分别为mA、mB电阻均为R的导体棒A、B,在B的右侧金属导轨中间放一内有炸药的物体C,当物体C内的炸药爆炸,使物体C分裂成两部分,质量为m1的部分沿桌面并垂直金属棒B向右飞出,另一块质量为m2的与B金属棒碰撞后粘合,使金属导体棒A经过t时间刚好达到最大速度并离开磁场,并沿接有小圆弧的与水平成θ的金属导轨上升,上升的最大高度为H(设没有能损失)。求
(1)炸药爆炸时释放的能量至少为多少?
(2)A金属导体棒在t时间内产生的热量为多少?
(3)作出A导体自开始运动至运动到最高点的过程的大致速度时间图象。
