时间:2017-08-07 15:31:13
1、选择题 如图所示,弹簧一端系在墙上O点,另一端自由伸长到B点,今将一小物体m压着弹簧(与弹簧未连接),将弹簧压缩到A点,然后释放,小物体能运动到C点静止,物体与水平地面间的动摩擦因数恒定。下列说法中正确的是( )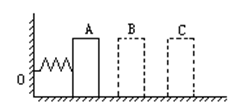
A.物体在B点受合外力为零
B.物体的速度从A到B越来越大,从B到C越来越小
C.物体从A到B加速度越来越小,从B到C加速度不变
D.物体从A到B先加速后减速,从B到C匀减速
参考答案:D
本题解析:物体在B点受到摩擦力的作用,故受合外力不为零 ,选项A错误;物体向右运动时,开始时弹力大于摩擦力,物体做加速运动,当弹力等于摩擦力时 加速度减为零,此时物体的速度最大,此位置在AB之间的某点,以后弹力小于摩擦力,物体做减速运动,经过B点以后物体只受摩擦力作用而做匀减速运动到C点停止,故物体从A到B先加速后减速,从B到C匀减速,选项D正确,BC错误;故选D.
考点:牛顿第二定律的应用.
本题难度:困难
2、计算题 质量,M=3kg的长木板放在光滑的水平面t在水平悄力F=11N作用下由静止开始 向右运动.如图所示,当速度达到1m/s2将质量m=4kg的物块轻轻放到本板的右端.已知物块与木板间摩擦因数μ=0.2,物块可视为质点.(g=10m/s2,).求: 
(1)物块刚放置木板上时,物块和木板加速度分别为多大?
(2)木板至少多长物块才能与木板最终保持相对静止?
(3)物块与木板相对静止后物块受到摩擦力大小?
参考答案:(1)2m/s2;1m/s2(2)0.5m;(3)6.29N
本题解析:(1)放上物块后,物体加速度
板的加速度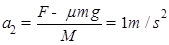
(2)当两物体达速度相等后保持相对静止,故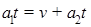
∴t=1秒
1秒内木板位移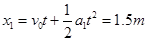
物块位移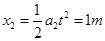
所以板长L=x1-x2=0.5m
(3)相对静止后,对整体 
对物块f=ma
∴f="44/7=6.29N"
考点:牛顿第二定律的综合应用.
本题难度:一般
3、选择题 如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为45°的光滑木板AB托住,小球恰好处于静止状态。当木板AB突然向下撤离的瞬间,小球的加速度大小为( )
A.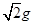
B.g
C.
D.0
参考答案:A
本题解析:木板撤去前,小球处于平衡态,受重力、支持力和弹簧的拉力,如图:
根据共点力平衡条件,有 ,
,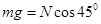 .解得:
.解得: ,
, .木板AB突然撤去后,支持力消失,重力和拉力不变,合力等于支持力N,方向与N反向,故加速度为
.木板AB突然撤去后,支持力消失,重力和拉力不变,合力等于支持力N,方向与N反向,故加速度为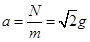 .故选A.
.故选A.
考点:本题考查了牛顿第二定律;力的合成与分解的运用.
本题难度:一般
4、选择题 如图所示是某商场安装的智能化电动扶梯,无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转。一顾客乘扶梯上楼,恰好经历了这两个过程。那么下列说法中正确的是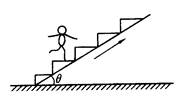
A.顾客始终受到静摩擦力的作用
B.顾客受到的支持力总是大于重力
C.扶梯对顾客作用力的方向先指向右上方,再竖直向上
D.扶梯对顾客作用力的方向先指向左下方,再竖直向上
参考答案:C
本题解析:顾客在匀速运动阶段,加速度为零,合力为零,顾客只受重力和支持力两个力,重力等于支持力,选项A、B错误;匀加速运动阶段,电梯对顾客的支持力竖直向上,静摩擦力水平向左,两者合力指向右侧斜上方.匀速运动阶段,电梯对顾客的支持力竖直向上,选项C正确。
考点:此题考查了牛顿运动定律。
本题难度:一般
5、计算题 如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行。传送带始终以速度v0=2m/s向右匀速运动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端。已知A、B质量均为1kg,B与传送带间的动摩擦因数为0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计。g取 10m/s2,sin37°=0.6。求: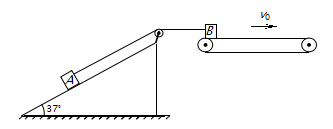
⑴B向右运动的总时间;
⑵B回到传送带左端时的速度;
⑶上述过程中B与传送带间因摩擦产生的总热量。
参考答案:(1)2s;(2)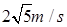 (3)
(3)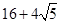 J
J
本题解析:⑴速度由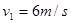 变化到
变化到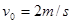 的过程
的过程
对B: 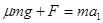
对A: 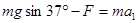
解得 加速度大小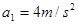
时间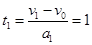 s
s
位移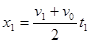
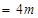
速度由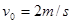 变化到0的过程
变化到0的过程
对B: 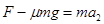
对A: 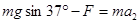
解得 加速度大小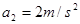
时间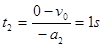
位移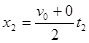
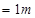
B向右运动的总时间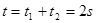
⑵B回到传送带左端过程
对B: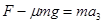
对A: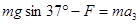
解得 加速度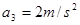
对B: 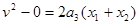
解得 速度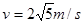
⑶B向右运动过程中,相对于传送带的路程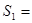
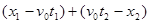
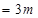
B向左运动时间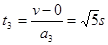
相对于传送带的路程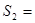
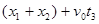
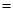
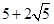 m
m
B与传送带间因摩擦产生的总热量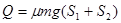 =
=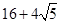 J
J
考点:牛顿第二定律的综合应用.
本题难度:一般