时间:2017-08-07 15:05:22
1、选择题 如题图所示,一个菱形框架绕着过对角线的竖直轴匀速转动,在两条边上各有一个质量相等的小球套在上面,整个过程小球相对框架没有发生滑动,A与B到轴的距离相等,则下列说法错误的是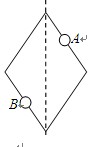
A.框架对A的弹力方向可能垂直框架向下
B.框架对B的弹力方向只能垂直框架向上
C.A与框架间可能没有摩擦力
D.A、B两球所受的合力大小相等
参考答案:C
本题解析:AB两个小球做匀速圆周运动,它们的合力充当向心力,轨道半径,质量,角速度均相等,所以向心力或者合力大小相等,D正确;框架对AB小球的弹力方向只能是垂直杆方向,因为合力指向圆心,所以对A球的支持力为垂直杆向下,对B球的支持力为垂直杆向上,AB正确;假设A与框架之间没有摩擦力,则A球只受到垂直杆向下的弹力和重力,所以合力不可能指向圆心,故A与框架之间一定存在摩擦力,C错误,
让选错误的,故选C
点评:关键是对小球受力分析,根据合力充当向心力判断,
本题难度:简单
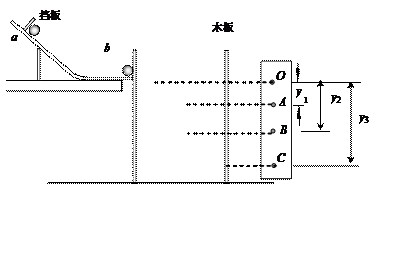
2、简答题 一水平放置的圆盘绕过其圆心的竖直轴匀速转动。盘边缘上固定一竖直的挡光片。盘转动时挡光片从一光电数字计时器的光电门的狭缝中经过,如图a所示。图b为光电数字计时器的示意图。光源A中射出的光可照到B中的接收器上。若A、B间的光路被遮断,显示器C上可显示出光线被遮住的时间。挡光片的宽度用螺旋测微器测得,结果如图c所示。圆盘直径用游标卡尺测得,结果如图d所示。由图可知,
小题1:挡光片的宽度是多少?
小题2:圆盘的直径为多少?
小题3:若光电数字计时器所显示的时间为50.0 ms,则圆盘转动的角速度为多少弧度/秒?(保留3位有效数字)。
参考答案:
小题1:宽度为10.242mm
小题2:圆盘直径为24.220cm
小题3: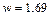 ?rad/s
?rad/s
本题解析:
小题1:由螺旋测微器与游标卡尺的读数规则可得两者的读数.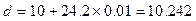 mm,
mm,
小题2: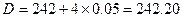 mm=24.220cm.
mm=24.220cm.
小题3:圆盘转动的角速度为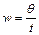 ,而
,而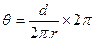
综合两式并代入数据可得: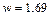 rad/s.
rad/s.
本题难度:一般
3、计算题 如图所示,曲面与半径为R=2.5m的竖直半圆组成光滑轨道.一个小球从A点斜向上抛,并在半圆最高点B水平进入轨道,然后沿曲面上升,最大高度达到h=10m。求小球抛出的速度 和位置s.
和位置s.
参考答案:14.1m/s 方向和水平方向成45°角? 10m
本题解析:小球由B到C:
得:
小球由A到B: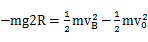
得:
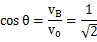
所以
即和水平方向成45°角
小球由A到B竖直方向: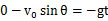
小球由A到B水平方向: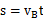
得:s=10m
本题难度:一般
4、计算题 如图7所示,小球A质量为m,固定在轻细绳L的一端,并随绳一起绕绳的另一端O点在竖直平面内做圆周运动。如果小球经过最高位置时,绳对球的作用力为拉力,拉力大小等于2倍球的重力。求: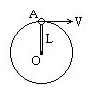
(1)球的速度大小。
(2)当小球经过最低点时速度为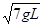 ,绳对球的作用力大小和球的向心加速度大小。
,绳对球的作用力大小和球的向心加速度大小。
参考答案:(1)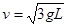 ;(2)7g。
;(2)7g。
本题解析:(1)小球A在最高点时,对球做受力分析,如图D-1所示。
重力mg; 拉力F=2mg?
根据小球做圆运动的条件,合外力等于向心力,即: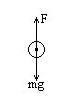
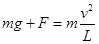 ? ............2分?
? ............2分?
F=2mg ②? ............1分
解①②两式,可得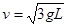 ............2分
............2分
(2)小球A在最低点时,对球做受力分析,如图D-2所示。
重力mg; 拉力F,设向上为正
根据小球做圆运动的条件,合外力等于向心力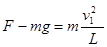 .........2分
.........2分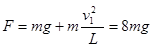 .........2分
.........2分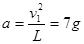 ............2分
............2分
本题难度:一般
5、选择题 (2011年江西八校联考)如图5-3-13所示,用长为L的轻绳把一个小铁球悬挂在高2L的O点处,小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,则有( )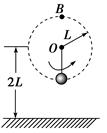
图5-3-13
A.小铁球在运动过程中轻绳的拉力最大为5mg
B.小铁球在运动过程中轻绳的拉力最小为mg
C.若运动中轻绳断开,则小铁球落到地面时的速度大小为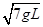
D.若小铁球运动到最低点轻绳断开,则小铁球落到地面时水平位移为2L
参考答案:C
本题解析:选C.小铁球以O为圆心在竖直平面内做圆周运动且恰能到达最高点B处,说明小铁球在最高点B处,轻绳的拉力最小为零,mg=mv2/L,v=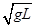 ;由机械能守恒定律得,小铁球运动到最低点时动能为mv
;由机械能守恒定律得,小铁球运动到最低点时动能为mv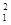 /2=mv2/2+mg·2L,在最低点轻绳的拉力最大,由牛顿第二定律得F-mg=mv
/2=mv2/2+mg·2L,在最低点轻绳的拉力最大,由牛顿第二定律得F-mg=mv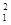 /L,联立解得轻绳的拉力最大为F=6mg;选项A、B错误;以地面为重力势能参考平面,小铁球在B点处的总机械能为mg·3L+
/L,联立解得轻绳的拉力最大为F=6mg;选项A、B错误;以地面为重力势能参考平面,小铁球在B点处的总机械能为mg·3L+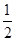 mv2=
mv2=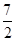 mgL,无论轻绳是在何处断开,小铁球的机械能总是守恒的,因此到达地面时的动能为
mgL,无论轻绳是在何处断开,小铁球的机械能总是守恒的,因此到达地面时的动能为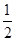 mv′2=
mv′2=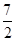 mgL,落到地面时的速度大小为v′=
mgL,落到地面时的速度大小为v′=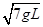 ,选项C正确;小铁球运动到最低点时速度v1=
,选项C正确;小铁球运动到最低点时速度v1=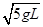 ,由s=v1t,L=
,由s=v1t,L=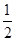 gt2,联立解得小铁球落到地面时的水平位移为s=
gt2,联立解得小铁球落到地面时的水平位移为s=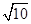 L,选项D错误.
L,选项D错误.
本题难度:一般