时间:2017-08-05 17:58:00
1、计算题 如图所示,游乐场上,两位同学各驾着一辆碰碰车迎面相撞,此后,两车以共同的速度运动。设甲同学和他的车的总质量为150 kg,碰撞前向右运动,速度的大小为4.5 m/s;乙同学和他的车的总质量为200 kg,碰撞前向左运动,速度的大小为3.7 m/s.求碰撞后两车共同的运动速度。
参考答案:解:本题的研究对象为两辆碰碰车(包括驾车的同学)组成的系统,在碰撞过程中此系统的内力远远大于所受的外力,外力可以忽略不计,满足动量守恒定律的适用条件,设甲同学的车碰撞前的运动方向为正方向,他和车的总质量m1=150 kg,碰撞前的速度v1=4.5m/s;乙同学和车的总质量m2=200 kg,碰撞前的速度v2=-3.7m/s;设碰撞后两车的共同速度为v,则
系统碰撞前的总动量为:p=m1v1+m2v2=150×4.5 kg·m/s+200×(-3.7)kg·m/s= -65 kg·m/s
碰撞后的总动量为p"=(m1+m2)v
根据动量守恒定律可知p=p",代入数据解得v=-0.186 m/s
即碰撞后两车以v=0.186 m/s的共同速度运动,运动方向向左
本题解析:
本题难度:一般
2、计算题 (附加题)
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°。

参考答案:解:设小球m的摆线长度为l,小球m在下落过程中与M相碰之前满足机械能守恒: ①
①
m和M碰撞过程满足: ②
②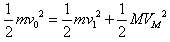 ③
③
联立②③得: ④
④
说明小球被反弹,而后小球又以反弹速度和小球M发生碰撞,满足: ?⑤
?⑤ ?⑥
?⑥
解得: ⑦
⑦
整理得: ⑧
⑧
所以: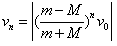 ⑨
⑨
而偏离方向为45°的临界速度满足: ⑩
⑩
联立①⑨⑩代入数据解得,当n=2时,
当n=3时,
所以最多碰撞3次
本题解析:
本题难度:困难
3、选择题 带有(1/4)光滑圆弧轨道、质量为M的滑车静止置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上滑车,当小球上行再返回,并脱离滑车时,以下说法可能正确的是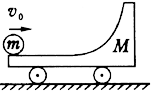
A.小球一定沿水平方向向左做平抛运动
B.小球可能沿水平方向向左做平抛运动
C.小球可能做自由落体运动
D.小球可能水平向右做平抛运动
参考答案:BCD
本题解析:小球滑上滑车,又返回,到离开滑车的整个过程,相当于小球与滑车发生弹性碰撞的过程.如果m<M,小球离开滑车向左做平抛运动;如果m=M,小球离开滑车做自由落体运动;如果m>M,小球离开滑车向右做平抛运动.
本题难度:简单
4、简答题 如图1-3所示,质量为m的木块可视为质点,置于质量也为m的木盒内,木盒底面水平,长l="0.8" m,木块与木盒间的动摩擦因数μ=0.5,木盒放在光滑的地面上,木块A以v0="5" m/s的初速度从木盒左边开始沿木盒底面向右运动,木盒原静止.当木块与木盒发生碰撞时无机械能损失,且不计碰撞时间,取g="10" m/s2.问:
小题1:木块与木盒无相对运动时,木块停在木盒右边多远的地方?
小题2:在上述过程中,木盒与木块的运动位移大小分别为多少?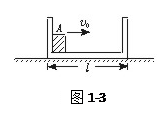
参考答案:
小题1:0.45 m
小题2:s盒="1.075" m?s块="1.425" m
本题解析: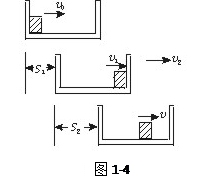
小题1:木块相对木盒运动及与木盒碰撞的过程中,木块与木盒组成的系统动量守恒,最终两者获得相同的速度,设共同的速度为v,木块通过的相对路程为s,则有:
mv0=2mv?① μmgs=
μmgs=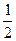 mv02-
mv02-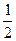 ·2mv2②
·2mv2②
由①②解得s="1.25" m
设最终木块距木盒右边为d,由几何关系可得:
d=s-l="0.45" m
小题2:从木块开始运动到相对木盒静止的过程中,木盒的运动分三个阶段:第一阶段,木盒向右做初速度为零的匀加速运动;第二阶段,木块与木盒发生弹性碰撞,因两者质量相等,所以交换速度;第三阶段,木盒做匀减速运动,木盒的总位移等于一、三阶段的位移之和.为了求出木盒运动的位移,我们画出状态示意图,如图1-4所示.
设第一阶段结束时,木块与木盒的速度分别为v1、v2,则:
mv0=mv1+mv2?③
μmgL=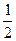 mv02-
mv02-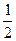 m(v12+v22)?④
m(v12+v22)?④
因在第二阶段中,木块与木盒转换速度,故第三阶段开始时木盒的速度应为v1,选木盒为研究对象
对第一阶段:μmgs1=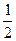 mv22?⑤
mv22?⑤
对第三阶段:μmgs2=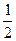 mv12-
mv12-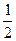 mv2?⑥
mv2?⑥
从示意图得s盒=s1+s2?⑦
s块=s盒+L-d?⑧
解得s盒="1.075" m?s块="1.425" m
本题难度:一般
5、选择题 A、B两球在光滑水平面上相向运动,两球相碰后有一球停止运动,则下述说法中正确的是
[? ]
A.若碰后,A球速度为0,则碰前A的动量一定大于B的动量
B.若碰后,A球速度为0,则碰前A的动量一定小于B的动量
C.若碰后,B球速度为0,则碰前A的动量一定大于B的动量
D.若碰后,B球速度为0,则碰前A的动量一定小于B的动量
参考答案:AD
本题解析:
本题难度:一般