时间:2017-08-05 17:54:18
1、选择题 A、B两球之间压缩一根轻弹簧,静置于光滑水平桌面上.已知A、B两球质量分别为2 m和m.当用板挡住A球而只释放B球时,B球被弹出落于距桌面水平距离为s的水平地面上,如图，问当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,B球的落地点距桌面距离为（ ）
A.
B.
s C.s D.
s
参考答案：D
本题解析：考点：动量守恒定律；平抛运动；机械能守恒定律．
专题：动量与动能定理或能的转化与守恒定律综合．
分析：A、B两球之间压缩一根轻弹簧，当用板挡住A球而只释放B球时，弹性势能完全转化为B球的动能，以一定的初速度抛出，借助于抛出水平位移可确定弹簧的弹性势能．当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，由动量守恒定律与机械能守恒定律可求出B球获得的速度，再由平抛运动规律可算出抛出的水平位移．
解答：解：当用板挡住A球而只释放B球时，B球做平抛运动．设高度为h，则有vB=s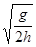
，所以弹性势能为E=
=
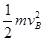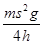当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，由动量守恒定律可得：0=2mvA-mvB 所以vA：vB=1：2．因此A球与B球获得的动能之比EkA：EkB=1：2．所以B球的获得动能为：
．
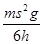那么B球抛出初速度为vB=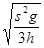
，则平抛后落地水平位移为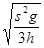
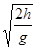=s
故选：D
点评：考查动量守恒定律、机械能守恒定律，及平抛运动规律．两种情况下，弹性势能完全相同．在弹簧恢复过程中弹性势能转化为动能．
本题难度：困难
2、计算题 （10分）光滑水平面上静置两个小木块1和2，其质量分别为m1＝1.0kg、m2＝4.0kg，它们中间用一根轻质弹簧相连。一颗水平飞行的子弹质量为m＝50.0g，以v0＝500m／s的速度在极短时间内射穿两木块，已知射穿木块1后子弹的速度变为原来的3／5，且子弹损失的动能为射穿木块2损失动能的2倍。求系统运动过程中弹簧的最大弹性势能。
参考答案：22.5J
本题解析：子弹与木块1系统，动量守恒mv0＝m·3v0／5＋m1v1?2分
同理，m·3v0／5＝m·v0／5＋m2v2?2分
当两小木块速度相等时（设为v），弹簧的弹性势能（E弹）最大?
m1v1＋m2v2＝（m1＋m2）v? 2分
E弹＝m1v12／2＋m2v22／2－（m1＋m2）v2／2? 2分
解得E弹＝22.5J? 2分
本题考查动量守恒定律，当子弹打入第一个木块时，弹簧来不及被压缩，所以木块2不参与碰撞，子弹和木块1动量守恒，找到初末状态列式求解，子弹打出后打进第二个木块，子弹和木块2的动量守恒，同理列式求解，在两次碰撞前后求出子弹损失的动能，根据2倍关系列式求解
本题难度：简单
3、计算题 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
参考答案：
本题解析：木板第一次与墙碰撞后,木板的速度反向,大小不变,此后木板向左做匀减速运动,重物向右做匀减速运动,最后木板和重物达到一共同速度为v,设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得
2mv0-mv0=3mv
设从第一次与墙碰撞到木板和重物具有共同速度v所用的时间为t1,
2μmgt1=mv-m(-v0)
由牛顿第二定律得2μmg=ma
式中a为木板的加速度.
在达到共同速度v时,木板离墙的距离l为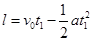
开始向右做匀速运动到第二次与墙碰撞的时间为
从第一次碰撞到第二次碰撞所经过的时间为
t=t1+t2
由以上各式得
本题难度：一般
4、计算题 (1)原子处于基态时最稳定，处于较高能级时会自发地向低能级跃迁．如图所示为氢原子的能级图．现让一束单色光照射到大量处于基态(量子数n＝1)的氢原子上，被激发的氢原子能自发地发出3种不同频率的色光，则照射氢原子的单色光的光子能量为多少eV？用这种光照射逸出功为4.54 eV的金属表面时，逸出的光电子的最大初动能是多少eV?
(2)静止的Li核俘获一个速度v1＝7.7×104 m/s的中子而发生核反应，生成两个新核．已知生成物中He的速度v2＝2.0×104 m/s，其方向与反应前中子速度方向相同．
①写出上述反应方程．
②求另一生成物的速度．
参考答案：：(1)12.09 7.55 (2)①Li＋n→H＋He
②1×103 m/s 运动方向与氦核相反
本题解析：：(1)由C＝3可知n＝3，故照射光的光子能量为E3－E1＝12.09 eV
由EK＝hν－W知EK＝(12.09－4.54) eV＝7.55 eV.
(2)①核反应方程式为Li＋n→H＋He.
②设中子、氦核、新核的质量分别为m1、m2、m3，
它们的速度分别为v1、v2、v3，
根据动量守恒有：m1v1＝m2v2＋m3v3
v3＝＝－1×103 m/s
负号说明新核运动方向与氦核相反．
本题难度：一般
5、简答题 如图所示，有一内表面光滑的金属盒，底面长为L=1.2m，质量为m1=1kg，放在水平面上，与水平面间的动摩擦因数为μ=0.2，在盒内最右端放一半径为r=0.1m的光滑金属球，质量为m2=1kg，现在盒的左端给盒施加一个水平冲量I=3N?s，（盒壁厚度，球与盒发生碰撞的时间和能量损失均忽略不计）．g取10m/s2，求：
（1）金属盒能在地面上运动多远？
（2）金属盒从开始运动到最后静止所经历的时间多长？
参考答案：（1）由于冲量作用，m1获得的速度为v=Im1=3m/s，
金属盒所受摩擦力为F=μ（m1+m2）g=4N，由于金属盒与金属球之间的碰撞没有能量损失，且金属盒和金属球的最终速度都为0，以金属盒和金属球为研究对象，由动能定理得：-Fs=0-12m1v2
解得：s=1.125m
（2）因r=0.1m，则当盒前进s1=1m时与球发生碰撞，设碰前盒的速度为v1，碰后速度为v1′，球碰后速度为v2，则对盒，应用动能定理：
-Fs1=12m1v21-12m1v2，解得v1=1m/s
由于碰撞中动量守恒、机械能守恒，有：
m1v1=m1v1′+m2v2，
12m1v21=12m1v′21+12m2v22
联立以上方程得：v1′=0，v2=1m/s．
当球前进1m时与盒发生第二次碰撞，碰撞前球的速度为1m/s，盒子的速度为0，碰撞后球的速度为0，盒子的速度变为v2=1m/s，
以金属盒为研究对象，利用动能定理得：
-Fs2=0-12m1v22，解得：s2=0.125m．
所以不会再与球碰，
则盒子运动时间可由动量定理给出：设盒子前进s1=1m所用时间为t1，前进s2=0.125m所用时间为t2，则：
-Ft1=m1v1-m1v，
-Ft2=0-m1v2，且v1=v2=1m/s
代入数据得：t1=0.5s，t2=0.25s
在盒两次运动之间还有一段时间t3为小球在运动，t3=s1/v2=1s
则金属盒从开始运动到最后静止所经历的时间t=t1+t2+t3=1.75s
答：
（1）金属盒能在地面上运动1.125m．
（2）金属盒从开始运动到最后静止所经历的时间是1.75s．
本题解析：
本题难度：一般