时间:2017-08-05 17:37:21
1、计算题 如图所示，竖直放置的圆弧轨道和水平轨道两部分相连。水平轨道的右侧有一质量为2m的滑块C与轻质弹簧的一端相连，弹簧的另一端固定在竖直的墙M上，弹簧处于原长时，滑块C静止在P点处；在水平轨道上方O处，用长为L的细线悬挂一质量为m的小球B，B球恰好与水平轨道相切，并可绕O点在竖直平面内摆动。质量为m的滑块A由圆弧轨道上静止释放，进入水平轨道与小球B发生碰撞，A、B碰撞前后速度发生交换。P点左方的轨道光滑、右方粗糙，滑块A、C与PM段的动摩擦因数均为μ=0.5，A、B、C均可视为质点，重力加速度为g。
（1）求滑块A从2L高度处由静止开始下滑，与B碰后瞬间B的速度；
（2）若滑块A能以与球B碰前瞬间相同的速度与滑块C相碰，A至少要从距水平轨道多高的地方开始释放？
（3）在（2）中算出的最小值高度处由静止释放A，经一段时间A与C相碰，设碰撞时间极短，碰后一起压缩弹簧，弹簧最大压缩量为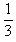
L，求弹簧的最大弹性势能。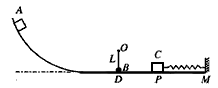 
参考答案：解：（1）对A，由机械能守恒得：mg2L=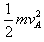
vA=2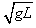
与B碰后速度交换，vB1=vA=2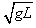
（2）要使滑块A能以与B碰前瞬间相同的速度与C碰撞，必须使小球B受A撞击后在竖直平面内完成一个完整的圆周运动后从左方撞击A，使A继续向右运动
设A从距水平面高为H的地方释放，与B碰前的速度为v0
对A，由机械能守恒得：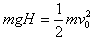
设小球B通过最高点的速度为vB，则它通过最高点的条件是：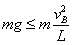
小球B从最低点到最高点的过程机械能守恒：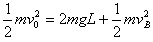
解得：H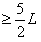
（3）从这个高度下滑的A与C碰撞前瞬间速度：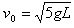
设A与C碰后瞬间的共同速度为v，由动量守恒：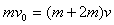
A、C一起压缩弹簧，由能量守恒定律。有：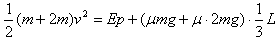
解得：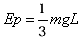
本题解析：
本题难度：困难
2、选择题 如图所示，固定的倾斜光滑杆上套有一个质量为m的圆环，圆环与竖直放置的轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，弹簧处于原长h．让圆环沿杆滑下，滑到杆的底端时速度为零．则在圆环下滑过程中（ ）
A．圆环机械能守恒
B．弹簧的弹性势能先增大后减小
C．弹簧的弹性势能变化了mgh
D．弹簧的弹性势能最大时圆环的动能最大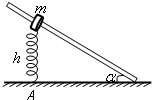
参考答案：A、圆环沿杆滑下，滑到杆的底端的过程中有两个力对圆环做功，即环的重力和弹簧的拉力；所以圆环的机械能不守恒，如果把圆环和弹簧组成的系统作为研究对象，则系统的机械能守恒，故A选项错误，
B、弹簧的弹性势能随弹簧的形变量的变化而变化，由图知弹簧先缩短后再伸长，故弹簧的弹性势能先增大再减小后增大才对．故B选项错误．
C、根据系统的机械能守恒，圆环的机械能减少了mgh，那么弹簧的机械能即弹性势能增大mgh．故C选项正确．
D、根据系统机械能守恒，弹簧弹性势能最大时圆环的速度等于零，故D选项错误．
故选C
本题解析：
本题难度：简单
3、计算题 如图所示．一个质量为m＝10kg的物体,?由1/4光滑圆弧轨道上端从静止开始下滑,?然后滑上粗糙水平面向右滑动2.0m的距离而停止．已知轨道半径R=0.8m,?g=10m/s2，?求：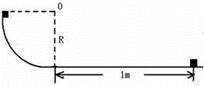
①物体滑至轨道底端时的速度?
②物体与水平面间的动摩擦因数μ?
参考答案：①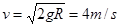
②?=0.4
本题解析：（1）由机械能守恒得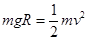
?
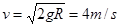
（2）由动能定理有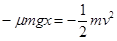
?=0.4
点评：本题难度较小，熟练掌握机械能守恒的条件，在水平面只有滑动摩擦力做功，由动能定理求解动摩擦因数
本题难度：简单
4、填空题 如图所示，在一个半径为R的半圆形光滑固定的轨道边缘，装着一个定滑轮，一轻绳跨过定滑轮，两端系着质量分别为m和M的物体（m＞2M），现将m从静止开始释放，m从轨道上边缘滑到此位置（α=60°）时的速率是______________。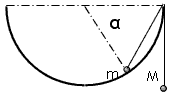
参考答案：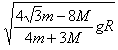
本题解析：
本题难度：一般
5、计算题 从倾角为θ的斜面顶点C处水平抛出一物体，初动能为10 J，物体到达斜面底端B处时，动能变为130 J。不计空气阻力，试求斜面的倾角。
参考答案：解：如图，取过B处的平面为零势能面，由于不考虑空气阻力，由机械能守恒定律得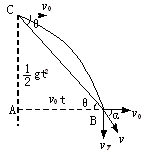 
mgh+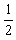
mv02=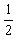
mv2，h=
在竖直方向上h=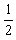
gt2，t=
=
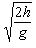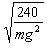
在△ABC中，tanθ=
=
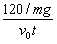
由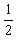
mv02=10得v0=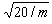
代入上式得tanθ=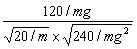
=
=
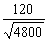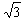
θ=arctan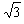
=60°
本题解析：
本题难度：困难