时间:2017-08-05 17:29:33
1、选择题 如图所示,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电量为q的带电粒子,在x轴上到原点的距离为x0的P点,以平行于y轴的初速度射入磁场.在磁场作用下沿垂直于y轴的方向射出磁场.不计重力的影响,由这些信息可以确定的是( )
A.能确定粒子通过y轴时的位置
B.能确定粒子速度的大小
C.能确定粒子在磁场中运动所经历的时间
D.能确定粒子带电性质
参考答案:
由题意可知,带电粒子要垂直于y轴离开磁场,可得知带电粒子逆时针运动,由左手定则可判断粒子带正电;带电粒子在磁场中的运动轨迹如图所示,可知离开磁场通过y轴时的位置的位置为y=x0;并得到运动的半径为R=x0,由半径公式R=mvqB可求出粒子的速度为v=qBx0m;带电粒子是垂直于y轴离开磁场的,顾可知带电粒子在磁场中运动了14圆周,即时间是14T,又因T=2πmqB,粒子的运动时间为πm2qB.四个选项全对.
故选:ABCD
本题解析:
本题难度:简单
2、选择题 如图,MN是磁感应强度为B的匀强磁场的边界,一带电微粒在纸面内从O点垂直于MN以速度v0射入磁场,最后落在C点,不计微粒的重力作用,则( )
A.落在C时速度vC方向垂直于MN
B.落在C时速度vC大于v0
C.增大v0,微粒将落在A点
D.减少v0,微粒在磁场中运动的时间不变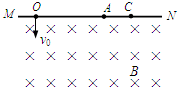
参考答案:A、因为微粒从O点开始垂直进入磁场,进入磁场后微粒做匀速圆周运动,故轨迹圆心在磁场边界MN上,MN与轨迹圆直径重合,根据几何关系可知微粒离开磁场时速度方向与MN垂直,故A正确.
B、因为微粒在磁场中做匀速圆周运动,故落在C点时的速度大小vC=v0,故B错误;
C、微粒在磁场中做匀速圆周运动,洛伦兹力提供万有引力qvB=mv2R?R=mvqB,微粒速度增大,运动轨迹的半径增大,微粒会打在C点右侧,而不会打在左侧的A点,故C错误;
D、微粒在磁场中正好运动12T,由洛伦兹力提供向心力可得T=2πRv=2πmvqBv=2πmqB,增大或减小微粒的速度不会影响微粒在磁场中运动的周期,故D正确.
故选AD.
本题解析:
本题难度:简单
3、计算题 如图所示,a点距坐标原点的距离为L,坐标平面内有边界过a点和坐标原点O的圆形匀强磁场区域,磁场方向垂直坐标平面向里,有一电子(质量为m、电荷量为e)从a点以初速度v0平行x轴正方向射入磁场区域,在磁场中运行,从x轴上的b点(图中未画出)射出磁场区域,此时速度方向与x轴的正方向之间的夹角为60°,求:
(1)磁场的磁感应强度;
(2)磁场区域的圆心O1的坐标;
(3)电子在磁场中运动的时间。
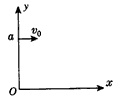
参考答案:解:(1)如图得R=2L
R=mv0/Be,B=

(2)x轴坐标x=aO1sin60°=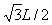
y轴坐标为y=L-aO1sin60°=L/2
O1点坐标为( L/2,L/2)
L/2,L/2)
(3)粒子在磁场中飞行时间为t=60°T/360°=2πL/3v0
本题解析:
本题难度:一般
4、计算题 (12分)如图所示,在相距为L,长为3L的平行金属板中间区域存在正交的匀强电场和匀强磁场,磁感应强度为B(方向未画),电场方向竖直向下。有一群均匀分布的同种带电粒子,以相同速度从两板间水平射入,经过时间t,粒子沿直线穿过该区域。若在粒子进入板间时,撤去电场保留磁场,粒子恰好全部打在板上。不计粒子的重力,不考虑粒子之间的相互作用,粒子对原来电场和磁场的影响不计。试求: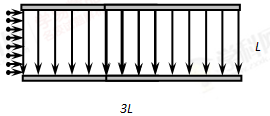
(1)该区域电场强度E大小;
(2)该粒子的比荷q/m ;
(3)若粒子进入时撤去磁场保留电场,则射出该区域的粒子数为总数的多少?
参考答案:(1)E=3BL/t (2)q/m=3/5Bt (3)只有10%的粒子能射出电场区域
本题解析:(1)由题意可知: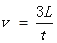
粒子通过速度选择器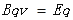
结合上面式子可知E=3BL/t
(2)若只有磁场存在时,恰好全部粒子落在极板上,
由勾股定理R2=(3L)2+(R-L)2
得到:R=5L 洛仑兹力提供向心力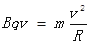
代入可得:q/m=3/5Bt
(3)若撤去磁场,保留电场,即粒子做类平抛运动,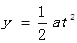
Eq=ma 代入可得:y=0.9L
即只有10%的粒子能射出电场区域
考点:带电粒子在复合场中的运动、带电粒子在电场中的运动、带电粒子在匀强磁场中的运动
本题难度:困难
5、选择题 一个重力不计的带电粒子垂直射入自左向右逐渐增强的磁场中,由于周围气体的阻碍作用,其运动轨迹恰为一段圆弧,则从如图所示中可以判断( )
A.粒子从A点射入,速率逐渐减小
B.粒子从A点射入,速率逐渐增大
C.粒子从B点射入,速率逐渐减小
D.粒子从B点射入,速率逐渐增大
参考答案:A
本题解析:
本题难度:一般